Un semn al unei linii perpendiculare și al unui plan. Ghid vizual (2019)
În această lecție, vom repeta teoria și vom demonstra teorema-atribut de perpendicularitate a unei drepte și a unui plan.
La începutul lecției, ne amintim definiția unei drepte perpendiculare pe un plan. În continuare, considerăm și demonstrăm teorema-atribut de perpendicularitate a unei drepte și a unui plan. Pentru a demonstra această teoremă, amintim proprietatea bisectoarei perpendiculare.
În continuare, rezolvăm câteva probleme privind perpendicularitatea unei drepte și a unui plan.
Subiect: Perpendicularitatea unei drepte și a unui plan
Lecția: Semn de perpendicularitate a unei drepte și a unui plan
În această lecție, vom repeta teoria și vom demonstra teorema-semn al perpendicularitatii unei drepte si a unui plan.
Definiție. Drept A se numește perpendicular pe un plan α dacă este perpendicular pe orice dreptă situată în acest plan.
Dacă o dreaptă este perpendiculară pe două drepte care se intersectează situate într-un plan, atunci este perpendiculară pe acel plan.
Dovada.
Să ni se dea un plan α. Două linii care se intersectează se află în acest plan. pși q. Drept A perpendicular pe linie p si direct q. Trebuie să dovedim că linia A este perpendiculară pe planul α, adică că linia a este perpendiculară pe orice dreaptă situată în planul α.
Aducere aminte.
Pentru a demonstra acest lucru, trebuie să ne amintim proprietățile bisectoarei perpendiculare pe un segment. Perpendiculară mijlocie R la segment AB este locul punctelor echidistante de capetele segmentului. Asta este, dacă ideea Cu se află pe bisectoarea perpendiculară p, atunci AC = BC.
Lasă punctul O- punctul de intersecție al unei drepte Ași planul α (Fig. 2). Fără a pierde generalitatea, vom presupune că liniile pși q se intersectează într-un punct O. Trebuie să demonstrăm perpendicularitatea dreptei A la o linie arbitrară m din planul α.
Să trecem prin punct O direct l, paralel cu linia m. Pe o linie dreaptă A pune deoparte segmentele OAși OV, și OA = OV, adică ideea O- mijlocul segmentului AB. Să tragem o linie dreaptă PL, 
.
Drept R perpendicular pe linie A(din condiție), 
(prin construcție). Mijloace, R AB. Punct R se află pe o linie dreaptă R. Mijloace, RA = RV.
Drept q perpendicular pe linie A(din condiție), 
(prin construcție). Mijloace, q- perpendiculara mijlocie pe segment AB. Punct Q se află pe o linie dreaptă q. Mijloace, QA =QB.
triunghiuri ARQși BPQ egal pe trei laturi (RA = RV, QA =QB, PQ- partea comună). Deci colțurile ARQși BPQ sunt egale.
triunghiuri DARPLși BPL egal în unghi și două laturi adiacente (∠ ARL= ∠BPL, RA = RV, PL- partea comună). Din egalitatea triunghiurilor obținem asta AL=BL.
Luați în considerare un triunghi ABL. Este echilateral deoarece AL=B.L.Într-un triunghi isoscel, mediana LO este și înălțimea, adică linia LO perpendicular AB.
Am înțeles asta A perpendicular pe linie euși deci drept m, Q.E.D.
puncte A, M, O se află pe o dreaptă perpendiculară pe planul α, iar punctele O, V, Sși D se află în planul α (Fig. 3). Care dintre următoarele unghiuri sunt drepte: ?
Decizie
Să luăm în considerare un unghi. Drept SA este perpendiculară pe planul α și, prin urmare, dreapta SA este perpendiculară pe orice dreaptă situată în planul α, inclusiv pe dreapta ÎN. Mijloace, .
Să luăm în considerare un unghi. Drept SA perpendicular pe linie OS, mijloace, .
Să luăm în considerare un unghi. Drept SA perpendicular pe linie OD, mijloace, . Luați în considerare un triunghi DAO. Un triunghi poate avea un singur unghi drept. Deci unghiul BARAJ- nu este directă.
Să luăm în considerare un unghi. Drept SA perpendicular pe linie OD, mijloace, .
Să luăm în considerare un unghi. Acesta este un unghi într-un triunghi dreptunghic BMO, nu poate fi drept, deoarece unghiul MoU- Drept.
Răspuns: 
.
Într-un triunghi ABC dat: , AC= 6 cm, soare= 8 cm, CM- mediană (Fig. 4). Prin vârf Cu direct SC perpendicular pe planul triunghiului ABC, și SC= 12 cm Localizați KM.
Decizie:
Să găsim lungimea AB conform teoremei lui Pitagora: (cm).
După proprietatea unui triunghi dreptunghic, punctul de mijloc al ipotenuzei M echidistant de vârfurile triunghiului. i.e SM = AM = VM, 
(cm).
Luați în considerare un triunghi KSM. Drept KS perpendicular pe plan ABC, care înseamnă KS perpendicular CM. Deci triunghiul KSM- dreptunghiular. Aflați ipotenuza KM din teorema lui Pitagora: (vezi).
1. Geometrie. Clasele 10-11: un manual pentru studenții instituțiilor de învățământ (nivel de bază și de profil) / I. M. Smirnova, V. A. Smirnov. - ediția a V-a, corectată și completată - M.: Mnemozina, 2008. - 288 p.: ill.
Sarcinile 1, 2, 5, 6 pagina 57
2. Definiți perpendicularitatea unei drepte și a unui plan.
3. Specificați o pereche în cub - o muchie și o față care sunt perpendiculare.
4. Punct La se află în afara planului unui triunghi isoscel ABCși echidistante de puncte LAși Cu. M- mijlocul bazei soare. Demonstrează că linia soare perpendicular pe plan AKM.
În această lecție, vom repeta teoria și vom demonstra teorema-atribut de perpendicularitate a unei drepte și a unui plan.
La începutul lecției, ne amintim definiția unei drepte perpendiculare pe un plan. În continuare, considerăm și demonstrăm teorema-atribut de perpendicularitate a unei drepte și a unui plan. Pentru a demonstra această teoremă, amintim proprietatea bisectoarei perpendiculare.
În continuare, rezolvăm câteva probleme privind perpendicularitatea unei drepte și a unui plan.
Subiect: Perpendicularitatea unei drepte și a unui plan
Lecția: Semn de perpendicularitate a unei drepte și a unui plan
În această lecție, vom repeta teoria și vom demonstra teorema-semn al perpendicularitatii unei drepte si a unui plan.
Definiție. Drept A se numește perpendicular pe un plan α dacă este perpendicular pe orice dreptă situată în acest plan.
Dacă o dreaptă este perpendiculară pe două drepte care se intersectează situate într-un plan, atunci este perpendiculară pe acel plan.
Dovada.
Să ni se dea un plan α. Două linii care se intersectează se află în acest plan. pși q. Drept A perpendicular pe linie p si direct q. Trebuie să dovedim că linia A este perpendiculară pe planul α, adică că linia a este perpendiculară pe orice dreaptă situată în planul α.
Aducere aminte.
Pentru a demonstra acest lucru, trebuie să ne amintim proprietățile bisectoarei perpendiculare pe un segment. Perpendiculară mijlocie R la segment AB este locul punctelor echidistante de capetele segmentului. Asta este, dacă ideea Cu se află pe bisectoarea perpendiculară p, atunci AC = BC.
Lasă punctul O- punctul de intersecție al unei drepte Ași planul α (Fig. 2). Fără a pierde generalitatea, vom presupune că liniile pși q se intersectează într-un punct O. Trebuie să demonstrăm perpendicularitatea dreptei A la o linie arbitrară m din planul α.
Să trecem prin punct O direct l, paralel cu linia m. Pe o linie dreaptă A pune deoparte segmentele OAși OV, și OA = OV, adică ideea O- mijlocul segmentului AB. Să tragem o linie dreaptă PL, .
Drept R perpendicular pe linie A(din condiție), (prin construcție). Mijloace, R AB. Punct R se află pe o linie dreaptă R. Mijloace, RA = RV.
Drept q perpendicular pe linie A(din condiție), (prin construcție). Mijloace, q- perpendiculara mijlocie pe segment AB. Punct Q se află pe o linie dreaptă q. Mijloace, QA =QB.
triunghiuri ARQși BPQ egal pe trei laturi (RA = RV, QA =QB, PQ- partea comună). Deci colțurile ARQși BPQ sunt egale.
triunghiuri DARPLși BPL egal în unghi și două laturi adiacente (∠ ARL= ∠BPL, RA = RV, PL- partea comună). Din egalitatea triunghiurilor obținem asta AL=BL.
Luați în considerare un triunghi ABL. Este echilateral deoarece AL=B.L.Într-un triunghi isoscel, mediana LO este și înălțimea, adică linia LO perpendicular AB.
Am înțeles asta A perpendicular pe linie euși deci drept m, Q.E.D.
puncte A, M, O se află pe o dreaptă perpendiculară pe planul α, iar punctele O, V, Sși D se află în planul α (Fig. 3). Care dintre următoarele unghiuri sunt drepte: ?
Decizie
Să luăm în considerare un unghi. Drept SA este perpendiculară pe planul α și, prin urmare, dreapta SA este perpendiculară pe orice dreaptă situată în planul α, inclusiv pe dreapta ÎN. Mijloace, .
Să luăm în considerare un unghi. Drept SA perpendicular pe linie OS, mijloace, .
Să luăm în considerare un unghi. Drept SA perpendicular pe linie OD, mijloace, . Luați în considerare un triunghi DAO. Un triunghi poate avea un singur unghi drept. Deci unghiul BARAJ- nu este directă.
Să luăm în considerare un unghi. Drept SA perpendicular pe linie OD, mijloace, .
Să luăm în considerare un unghi. Acesta este un unghi într-un triunghi dreptunghic BMO, nu poate fi drept, deoarece unghiul MoU- Drept.
Răspuns: .
Într-un triunghi ABC dat: , AC= 6 cm, soare= 8 cm, CM- mediană (Fig. 4). Prin vârf Cu direct SC perpendicular pe planul triunghiului ABC, și SC= 12 cm Localizați KM.
Decizie:
Să găsim lungimea AB conform teoremei lui Pitagora: (cm).
După proprietatea unui triunghi dreptunghic, punctul de mijloc al ipotenuzei M echidistant de vârfurile triunghiului. i.e SM = AM = VM, (cm).
Luați în considerare un triunghi KSM. Drept KS perpendicular pe plan ABC, care înseamnă KS perpendicular CM. Deci triunghiul KSM- dreptunghiular. Aflați ipotenuza KM din teorema lui Pitagora: (vezi).
1. Geometrie. Clasele 10-11: un manual pentru studenții instituțiilor de învățământ (nivel de bază și de profil) / I. M. Smirnova, V. A. Smirnov. - ediția a V-a, corectată și completată - M.: Mnemozina, 2008. - 288 p.: ill.
Sarcinile 1, 2, 5, 6 pagina 57
2. Definiți perpendicularitatea unei drepte și a unui plan.
3. Specificați o pereche în cub - o muchie și o față care sunt perpendiculare.
4. Punct La se află în afara planului unui triunghi isoscel ABCși echidistante de puncte LAși Cu. M- mijlocul bazei soare. Demonstrează că linia soare perpendicular pe plan AKM.
Să reparăm conceptul de perpendicularitate a unei drepte și a unui plan cu un rezumat al lecției. Să oferim o definiție generală, să formulăm și să dăm dovezi ale teoremei și să rezolvăm mai multe probleme pentru a consolida materialul.
Din cursul geometriei se știe: două drepte sunt considerate perpendiculare când se intersectează la un unghi de 90 o.
In contact cu
Colegi de clasa
Partea teoretică
Revenind la studiul caracteristicilor figurilor spațiale, vom aplica un nou concept.
Definiție:
Se va spune că o dreaptă este perpendiculară pe un plan atunci când este perpendiculară pe o dreaptă de pe o suprafață care trece în mod arbitrar prin punctul de intersecție.
Cu alte cuvinte, dacă segmentul „AB” este perpendicular pe planul α, atunci unghiul de intersecție cu orice segment trasat de-a lungul suprafeței date prin „C”, punctul de trecere al lui „AB” prin planul α, va fi 90 o.
Din cele de mai sus rezultă teorema privind semnul perpendicularității unei drepte și a unui plan:
dacă linia trasată prin plan este perpendiculară pe două drepte trasate pe planul prin punctul de intersecție, atunci este perpendiculară pe întregul plan.
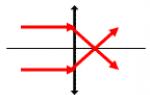
Cu alte cuvinte, dacă în Figura 1 unghiurile ACD și ACE sunt de 90 de grade, atunci unghiul ACF va fi și el de 90 de grade. Vezi figura 3.
Dovada
Conform condițiilor teoremei, dreapta „a” este trasată perpendicular pe drepte dși e. Cu alte cuvinte, unghiurile ACD și ACE sunt de 90°. Vom da dovezi pe baza proprietăților egalității triunghiurilor. Vezi figura 3.
Prin punctul C trecând linia A trageți o dreaptă prin planul α fîntr-o direcție arbitrară. Dăm dovadă că va fi perpendicular pe segmentul AB sau unghiul ACF va fi de 90 o.
Pe o linie dreaptă A puneți deoparte segmentele de aceeași lungime AC și AB. Desenați o linie pe suprafața α Xîntr-o direcție arbitrară și care nu trece prin intersecția din punctul „C”. Linia „x” trebuie să traverseze liniile e, d și f.
Conectați punctele F, D și E cu punctele A și B cu linii drepte.
Luați în considerare două triunghiuri ACE și BCE. Conform conditiilor de constructie:
- Există două laturi identice AC și BC.
- Au o parte comună CE în partea de jos.
- Două unghiuri egale ACE și BCE - 90 de grade fiecare.
Prin urmare, conform condițiilor de egalitate a triunghiurilor, dacă avem două laturi egale și același unghi între ele, atunci aceste triunghiuri sunt egale. Din egalitatea triunghiurilor rezultă că laturile AE și BE sunt egale.
În consecință, se demonstrează egalitatea triunghiurilor ACD și BCD, cu alte cuvinte, egalitatea laturilor AD și BD.
Acum luați în considerare două triunghiuri AED și BED. Din egalitatea dovedită anterior a triunghiurilor rezultă că aceste figuri au aceleași laturi AE cu BE și AD cu BD. O parte a ED este partajată. Din condiția de egalitate a triunghiurilor definite de trei laturi, rezultă că unghiurile ADE și BDE sunt egale.
Suma unghiurilor ADE și ADF este de 180 o. Suma unghiurilor BDE și BDF va fi de asemenea 180 o. Deoarece unghiurile ADE și BDE sunt egale, unghiurile ADF și BDF sunt de asemenea egale.
Luați în considerare două triunghiuri ADF și BDF. Au două laturi egale AD și BD (demonstrat mai devreme), DF o latură comună și un unghi egal între ele ADF și BDF. Prin urmare, aceste triunghiuri au laturile de aceeași lungime. Adică, latura BF are aceeași lungime ca și latura AF.
Dacă luăm în considerare triunghiul AFB, atunci acesta va fi isoscel (AF este egal cu BF), iar linia FC este mediana, deoarece conform condițiilor de construcție, latura AC este egală cu latura BC. Prin urmare, unghiul ACF este de 90 de grade. Ceea ce urma să fie dovedit.
O consecință importantă a teoremei de mai sus este afirmația:
dacă două paralele intersectează planul și unul dintre ele face un unghi de 90 o, atunci al doilea trece și el prin plan la un unghi de 90 o.
Conform condițiilor problemei, a și b sunt paralele. Vezi Figura 4. Linia a este perpendiculară pe suprafața α. Rezultă că linia b va fi și perpendiculară pe suprafața α.
Pentru a demonstra prin două puncte de intersecție a unor drepte paralele cu un plan, trasăm o dreaptă pe suprafață c. Conform teoremei pe o dreaptă perpendiculară pe un plan, unghiul DAB va fi de 90 o. Din proprietățile dreptelor paralele rezultă că și unghiul ABF va fi de 90 o. Prin urmare, prin definiție, linia b va fi perpendiculară pe suprafața α.
Utilizarea teoremei pentru a rezolva probleme
Pentru a fixa materialul, folosind condițiile fundamentale de perpendicularitate a unei drepte și a unui plan, vom rezolva mai multe probleme.
Sarcina 1
Condiții. Din punctul A, construiți o dreaptă perpendiculară pe planul α. Vezi figura 5.
Desenați o linie arbitrară b pe suprafața α. Prin dreapta b și punctul A construim suprafața β. Desenați segmentul AB de la punctul A la dreapta b. Din punctul B de pe suprafața α trageți o dreaptă perpendiculară c.
De la punctul A la linie cu scade perpendiculara AC. Să demonstrăm că această dreaptă va fi perpendiculară pe plan.
Pentru a demonstra prin punctul C de pe suprafața α trasăm o dreaptă d paralelă cu b, iar prin dreapta c iar punctul A construim un plan. Linia AC este perpendiculară pe dreapta c după condiția de construcție și perpendiculară pe dreapta d, ca o consecință a celor două drepte paralele din teorema perpendicularității, întrucât prin condiție dreapta b este perpendiculară pe suprafața γ.
Prin urmare, prin definiția perpendicularității unei drepte și a unui plan, segmentul construit AC este perpendicular pe suprafața α.
Sarcina #2
Condiții. Segmentul AB este perpendicular pe planul α. Triunghiul BDF este situat pe suprafața α și are următorii parametri:
- unghiul DBF va fi de 90 o
- latură BD=12 cm;
- latura BF=16 cm;
- BC este mediana.
Vezi figura 6.
Aflați lungimea segmentului AC dacă AB = 24 cm.
Decizie. După teorema lui Pitagora, ipotenuza sau latura DF este egală cu rădăcina pătrată a sumei pătratelor catetelor. Lungimea pătratului BD este 144 și, în consecință, pătratul BC va fi 256. Suma este 400; luând rădăcina pătrată, obținem 20.
Mediana BC într-un triunghi dreptunghic împarte ipotenuza în două părți egale și are lungimea egală cu aceste segmente, adică BC \u003d DC \u003d CF \u003d 10.
Se folosește din nou teorema lui Pitagora și obținem: ipotenuza C = 26, care este rădăcina pătrată a lui 675, suma pătratelor catetelor este 576 (AB = 24 la pătrat) și 100 (BC = 10 la pătrat).
Răspuns: Lungimea segmentului AC este de 26 cm.
