Jak najít základnu s hranolu. Základna pravého trojbokého hranolu
Vaše soukromí je pro nás důležité. Z tohoto důvodu jsme vyvinuli Zásady ochrany osobních údajů, které popisují, jak používáme a uchováváme vaše informace. Přečtěte si prosím naše zásady ochrany osobních údajů a dejte nám vědět, pokud máte nějaké dotazy.
Shromažďování a používání osobních údajů
Osobní údaje jsou údaje, které lze použít k identifikaci nebo kontaktování konkrétní osoby.
Kdykoli nás budete kontaktovat, můžete být požádáni o poskytnutí svých osobních údajů.
Níže jsou uvedeny některé příklady typů osobních údajů, které můžeme shromažďovat, a jak takové informace můžeme používat.
Jaké osobní údaje shromažďujeme:
- Když odešlete žádost na stránce, můžeme shromažďovat různé informace, včetně vašeho jména, telefonního čísla, e-mailové adresy atd.
Jak používáme vaše osobní údaje:
- Osobní údaje, které shromažďujeme, nám umožňují kontaktovat vás a informovat vás o jedinečných nabídkách, akcích a dalších akcích a nadcházejících událostech.
- Čas od času můžeme použít vaše osobní údaje k zasílání důležitých upozornění a zpráv.
- Osobní údaje můžeme také používat pro interní účely, jako je provádění auditů, analýzy dat a různé výzkumy, abychom zlepšili služby, které poskytujeme, a abychom vám poskytli doporučení týkající se našich služeb.
- Pokud se zúčastníte slosování, soutěže nebo podobné pobídky, můžeme použít vámi poskytnuté informace ke správě takových programů.
Zpřístupnění třetím stranám
Informace, které od vás obdržíme, nesdělujeme třetím stranám.
Výjimky:
- V případě, že je nutné - v souladu se zákonem, soudním řádem, v soudním řízení a/nebo na základě veřejných žádostí nebo žádostí státních orgánů na území Ruské federace - zveřejnit Vaše osobní údaje. Můžeme také zveřejnit informace o vás, pokud usoudíme, že takové zveřejnění je nezbytné nebo vhodné z důvodu bezpečnosti, vymáhání práva nebo jiného veřejného zájmu.
- V případě reorganizace, fúze nebo prodeje můžeme osobní údaje, které shromažďujeme, předat příslušné třetí straně, nástupci.
Ochrana osobních údajů
Přijímáme opatření – včetně administrativních, technických a fyzických – k ochraně vašich osobních údajů před ztrátou, krádeží a zneužitím, jakož i před neoprávněným přístupem, zveřejněním, pozměněním a zničením.
Zachování vašeho soukromí na úrovni společnosti
Abychom zajistili, že jsou vaše osobní údaje v bezpečí, sdělujeme našim zaměstnancům postupy ochrany osobních údajů a zabezpečení a přísně vynucujeme postupy ochrany osobních údajů.
V prostorové geometrii při řešení problémů s hranoly často nastává problém s výpočtem plochy stran nebo ploch, které tvoří tyto trojrozměrné obrazce. Tento článek je věnován problematice stanovení plochy základny hranolu a jeho bočního povrchu.
Figurový hranol
Než přistoupíme k úvahám o vzorcích pro oblast základny a povrchu hranolu toho či onoho druhu, je nutné pochopit, o jakém druhu postavy mluvíme.
Hranol v geometrii je prostorový obrazec sestávající ze dvou rovnoběžných mnohoúhelníků, které jsou si navzájem rovné, a několika čtyřúhelníků nebo rovnoběžníků. Počet posledně jmenovaných je vždy roven počtu vrcholů jednoho polygonu. Pokud je například obrazec tvořen dvěma rovnoběžnými n-úhelníky, pak bude počet rovnoběžníků n.
Spojovací n-úhelníky rovnoběžníku se nazývají strany hranolu a jejich celková plocha je plocha bočního povrchu obrázku. Samotné n-úhelníky se nazývají báze.
Výše uvedený obrázek ukazuje příklad papírového hranolu. Žlutý obdélník je jeho horní základna. Na druhé základně stejného obrázku stojí. Červené a zelené obdélníky jsou boční plochy.
Jaké jsou hranoly?
Existuje několik typů hranolů. Všechny se od sebe liší pouze ve dvou parametrech:
- typ n-úhelníku tvořícího báze;
- úhel mezi n-úhelníkem a bočními plochami.
Například, pokud jsou základny trojúhelníky, pak se hranol nazývá trojúhelníkový hranol, pokud čtyřúhelník, jako na předchozím obrázku, pak se obrazec nazývá čtyřboký hranol a tak dále. Navíc n-úhelník může být konvexní nebo konkávní, pak se tato vlastnost přidává i do názvu hranolu.
Úhel mezi bočními plochami a základnou může být buď přímý, nebo ostrý nebo tupý. V prvním případě mluví o obdélníkovém hranolu, ve druhém - o šikmém nebo šikmém.
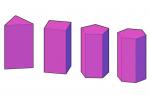
Pravidelné hranoly se rozlišují na zvláštní typ obrazců. Mezi ostatními hranoly mají nejvyšší symetrii. Správný bude pouze tehdy, bude-li obdélníkový a jeho základna je pravidelný n-úhelník. Obrázek níže ukazuje sadu pravidelných hranolů, ve kterých se počet stran n-úhelníku mění od tří do osmi.

Povrch hranolu
Pod povrchem uvažovaného útvaru libovolného typu se rozumí souhrn všech bodů, které patří k plochám hranolu. Je vhodné studovat povrch hranolu zvažováním jeho vývoje. Níže je uveden příklad takového rozmítání pro trojúhelníkový hranol.

Je vidět, že celou plochu tvoří dva trojúhelníky a tři obdélníky.
V případě hranolu obecného typu se jeho povrch bude skládat ze dvou n-gonálních základen a n čtyřúhelníků.
Podívejme se podrobněji na problém výpočtu povrchové plochy hranolů různých typů.
Základní plocha hranolu
Snad nejjednodušším úkolem při práci s hranoly je problém najít základní plochu pravidelné postavy. Protože je tvořen n-úhelníkem, pro který jsou všechny úhly a délky stran stejné, je vždy možné jej rozdělit na shodné trojúhelníky, u kterých jsou známé úhly a strany. Celková plocha trojúhelníků bude plocha n-úhelníku.
Dalším způsobem, jak určit část plochy povrchu hranolu (základny), je použít dobře známý vzorec. Vypadá to takto:
S n = n/4*a 2 *ctg(pi/n)
To znamená, že plocha S n n-úhelníku je jednoznačně určena na základě znalosti délky jeho strany a. Určitým problémem při výpočtu vzorce může být výpočet kotangens, zvláště když n>4 (pro n≤4 jsou hodnoty kotangens tabulkové údaje). K určení této goniometrické funkce se doporučuje použít kalkulačku.
Při zadávání geometrického problému byste měli být opatrní, protože možná budete muset najít oblast základny hranolu. Potom by se hodnota získaná vzorcem měla vynásobit dvěma.
Základní plocha trojúhelníkového hranolu
Na příkladu trojúhelníkového hranolu zvažte, jak můžete najít oblast základny tohoto obrázku.
Nejprve zvažte jednoduchý případ - pravidelný hranol. Plocha základny se vypočítá podle vzorce uvedeného v odstavci výše, musíte do ní nahradit n \u003d 3. Dostaneme:
S 3 = 3/4*a 2 *ctg(pi/3) = 3/4*a 2 *1/√3 = √3/4*a 2
Zbývá dosadit do výrazu konkrétní hodnoty délky strany a rovnostranného trojúhelníku, abychom získali plochu základny.
Nyní předpokládejme, že máme hranol, jehož základna je libovolný trojúhelník. Jeho dvě strany a a b a úhel mezi nimi α jsou známé. Tento obrázek je uveden níže.

Jak v tomto případě najít oblast základny trojúhelníkového hranolu? Je třeba si uvědomit, že plocha jakéhokoli trojúhelníku se rovná polovině součinu strany a výšce snížené na tuto stranu. Obrázek ukazuje výšku h ke straně b. Délka h odpovídá součinu sinusového úhlu alfa a délky strany a. Pak je plocha celého trojúhelníku:
S = 1/2*b*h = 1/2*b*a*sin(α)
Toto je základní plocha zobrazeného trojúhelníkového hranolu.
Boční povrch
Přišli jsme na to, jak najít oblast základny hranolu. Boční plocha tohoto obrázku se vždy skládá z rovnoběžníků. U přímých hranolů se rovnoběžníky stanou obdélníky, takže je snadné vypočítat jejich celkovou plochu:
S = ∑ i=1 n (a i *b)
Zde b je délka boční hrany a i je délka strany i-tého obdélníku, která se shoduje s délkou strany n-úhelníku. V případě pravidelného n-gonálního hranolu dostaneme jednoduchý výraz:
Pokud je hranol nakloněný, pak pro určení plochy jeho bočního povrchu je třeba provést kolmý řez, vypočítat jeho obvod P sr a vynásobit ho délkou bočního žebra.

Výše uvedený obrázek ukazuje, jak by měl být tento řez proveden pro šikmý pětiboký hranol.
Oblast bočního povrchu hranolu. Ahoj! V této publikaci budeme analyzovat skupinu úloh ze stereometrie. Uvažujme kombinaci těles – hranol a válec. Tento článek v tuto chvíli doplňuje celou sérii článků souvisejících s úvahami o typech úloh ve stereometrii.
Pokud se v bance úkolů objeví nové úkoly, pak samozřejmě budou na blogu v budoucnu přibývat. Ale co už je, je docela dost na to, abyste se v rámci zkoušky naučili řešit všechny problémy s krátkou odpovědí. Materiálu vystačí na roky dopředu (program v matematice je statický).
Uvedené úlohy se týkají výpočtu plochy hranolu. Podotýkám, že níže uvažujeme přímý hranol (a podle toho také přímý válec).
Aniž bychom znali nějaké vzorce, chápeme, že boční povrch hranolu jsou všechny jeho boční strany. V přímém hranolu jsou boční plochy obdélníky.
Boční plocha takového hranolu se rovná součtu ploch všech jeho bočních ploch (tj. obdélníků). Pokud mluvíme o pravidelném hranolu, do kterého je vepsán válec, pak je jasné, že všechny plochy tohoto hranolu jsou ROVNÉ obdélníky.
Formálně lze boční plochu pravidelného hranolu vyjádřit takto:

27064. Pravidelný čtyřboký hranol je opsán kolem válce, jehož základní poloměr a výška jsou rovné 1. Najděte plochu boční plochy hranolu.

Boční plocha tohoto hranolu se skládá ze čtyř obdélníků o stejné ploše. Výška čela je rovna 1, hrana základny hranolu je rovna 2 (to jsou dva poloměry válce), proto je plocha boční strany rovna:
Boční povrch:
73023. Najděte plochu bočního povrchu pravidelného trojúhelníkového hranolu opsaného kolem válce, jehož základní poloměr je √0,12 a jehož výška je 3.

Plocha boční plochy tohoto hranolu se rovná součtu ploch tří bočních ploch (obdélníků). Chcete-li najít oblast boční plochy, musíte znát její výšku a délku základní hrany. Výška je tři. Najděte délku okraje základny. Zvažte projekci (pohled shora):

Máme pravidelný trojúhelník, do kterého je vepsána kružnice o poloměru √0,12. Z pravoúhlého trojúhelníku AOC najdeme AC. A pak AD (AD=2AC). Podle definice tečny:
Takže AD \u003d 2AC \u003d 1.2. Plocha bočního povrchu se tedy rovná:
27066. Najděte plochu bočního povrchu pravidelného šestibokého hranolu opsaného kolem válce, jehož základní poloměr je √75 a jehož výška je 1.

Požadovaná plocha se rovná součtu ploch všech bočních ploch. U pravidelného šestibokého hranolu jsou boční plochy stejné obdélníky.
Chcete-li najít oblast obličeje, musíte znát jeho výšku a délku základní hrany. Výška je známá, rovná se 1.
Najděte délku okraje základny. Zvažte projekci (pohled shora):

Máme pravidelný šestiúhelník, do kterého je vepsána kružnice o poloměru √75.
Uvažujme pravoúhlý trojúhelník ABO. Známe nohu OB (to je poloměr válce). můžeme určit i úhel AOB, je roven 300 (trojúhelník AOC je rovnostranný, OB je osa).
Použijme definici tečny v pravoúhlém trojúhelníku:
AC \u003d 2AB, protože OB je medián, to znamená, že rozděluje AC na polovinu, což znamená AC \u003d 10.
Plocha boční plochy je tedy 1∙10=10 a plocha boční plochy je:
76485. Najděte plochu bočního povrchu pravidelného trojúhelníkového hranolu vepsaného do válce, jehož základní poloměr je 8√3 a jehož výška je 6.

Plocha boční plochy určeného hranolu tří stejně velkých ploch (obdélníků). Pro zjištění plochy je potřeba znát délku hrany podstavy hranolu (známe výšku). Pokud vezmeme v úvahu projekci (půdorys), pak máme pravidelný trojúhelník vepsaný do kruhu. Strana tohoto trojúhelníku je vyjádřena poloměrem jako:
Podrobnosti tohoto vztahu. Takže se to bude rovnat
![]()
Potom je plocha boční plochy rovna: 24∙6=144. A požadovaná oblast:
245354. Pravidelný čtyřboký hranol je opsán poblíž válce, jehož základní poloměr je 2. Boční povrch hranolu je 48. Najděte výšku válce.
hranol je mnohostěn, jehož dvě plochy jsou stejných n-úhelníků (důvody) , ležící v rovnoběžných rovinách a zbývajících n ploch jsou rovnoběžníky (boční strany) . Boční žebro hranolu je strana boční plochy, která nepatří k základně.
Nazývá se hranol, jehož boční hrany jsou kolmé k rovinám podstav rovný hranol (obr. 1). Pokud boční hrany nejsou kolmé k rovinám podstav, pak se nazývá hranol šikmý . opravit Hranol je rovný hranol, jehož základnou jsou pravidelné mnohoúhelníky.
Výška hranol se nazývá vzdálenost mezi rovinami podstav. Úhlopříčka Hranol je úsečka spojující dva vrcholy, které nepatří ke stejné ploše. diagonální řez Nazývá se řez hranolem rovinou procházející dvěma bočními hranami, které nepatří ke stejné ploše. Kolmý řez nazývaný řez hranolem rovinou kolmou k boční hraně hranolu.
Boční povrchová plocha hranol je součet ploch všech bočních ploch. Celá plocha nazývá se součet ploch všech ploch hranolu (tj. součet ploch bočních ploch a ploch podstav).
Pro libovolný hranol platí vzorce:
![]()
kde l je délka bočního žebra;
H- výška;
P
Q
S strana
S plný
S hlavní je plocha základen;
PROTI je objem hranolu.
Pro přímý hranol platí následující vzorce:
kde p- obvod základny;
l je délka bočního žebra;
H- výška.
Rovnoběžné Hranol se nazývá hranol, jehož základnou je rovnoběžník. Kvádr, jehož boční hrany jsou kolmé k základnám, se nazývá Přímo (obr. 2). Pokud boční hrany nejsou kolmé k základnám, pak se nazývá rovnoběžnostěn šikmý . Pravý rovnoběžnostěn, jehož základnou je obdélník, se nazývá obdélníkový. Pravoúhlý rovnoběžnostěn, ve kterém jsou všechny hrany stejné, se nazývá krychle.
Tváře rovnoběžnostěnu, které nemají společné vrcholy, se nazývají naproti . Délky hran vycházejících z jednoho vrcholu se nazývají Měření rovnoběžnostěn. Protože krabice je hranol, jsou její hlavní prvky definovány stejným způsobem, jako jsou definovány pro hranoly.
Věty.
1. Úhlopříčky kvádru se protínají v jednom bodě a půlí jej.
2. V pravoúhlém rovnoběžnostěnu se čtverec délky úhlopříčky rovná součtu čtverců jeho tří rozměrů: ![]()
3.  Všechny čtyři úhlopříčky pravoúhlého rovnoběžnostěnu jsou si navzájem rovné.
Všechny čtyři úhlopříčky pravoúhlého rovnoběžnostěnu jsou si navzájem rovné.
Pro libovolný rovnoběžnostěn platí následující vzorce:
![]()
kde l je délka bočního žebra;
H- výška;
P je obvod kolmého řezu;
Q– Plocha kolmého řezu;
S strana je plocha bočního povrchu;
S plný je celková plocha povrchu;
S hlavní je plocha základen;
PROTI je objem hranolu.
Pro pravý rovnoběžnostěn platí následující vzorce:
kde p- obvod základny;
l je délka bočního žebra;
H je výška pravého rovnoběžnostěnu.
Pro pravoúhlý rovnoběžnostěn platí následující vzorce:
![]() (3)
(3)
kde p- obvod základny;
H- výška;
d- diagonální;
a,b,c– měření rovnoběžnostěnu.
Správné vzorce pro kostku jsou:
kde A je délka žebra;
d je úhlopříčka krychle.
Příklad 1Úhlopříčka obdélníkového kvádru je 33 dm a jeho rozměry jsou vztaženy jako 2 : 6 : 9. Najděte rozměry kvádru.
Rozhodnutí. Pro zjištění rozměrů rovnoběžnostěnu použijeme vzorec (3), tzn. skutečnost, že druhá mocnina přepony kvádru je rovna součtu druhých mocnin jeho rozměrů. Označit podle k koeficient proporcionality. Pak se rozměry rovnoběžnostěnu budou rovnat 2 k, 6k a 9 k. Pro data problému napíšeme vzorec (3):
Řešení této rovnice pro k, dostaneme:
Rozměry kvádru jsou tedy 6 dm, 18 dm a 27 dm.
Odpovědět: 6 dm, 18 dm, 27 dm.
Příklad 2 Najděte objem nakloněného trojúhelníkového hranolu, jehož základna je rovnostranný trojúhelník o straně 8 cm, pokud je boční hrana rovna straně základny a je skloněna pod úhlem 60º k základně.
 Rozhodnutí
.
Udělejme nákres (obr. 3).
Rozhodnutí
.
Udělejme nákres (obr. 3).
Abyste našli objem nakloněného hranolu, musíte znát oblast jeho základny a výšky. Plocha základny tohoto hranolu je plocha rovnostranného trojúhelníku o straně 8 cm. Vypočítejme to:
![]()
Výška hranolu je vzdálenost mezi jeho základnami. Z vrchu ALE 1 horní podstavy spustíme kolmici k rovině spodní podstavy ALE 1 D. Jeho délka bude výška hranolu. Zvažte D ALE 1 INZERÁT: protože se jedná o úhel sklonu bočního žebra ALE 1 ALE do základní roviny ALE 1 ALE= 8 cm.Z tohoto trojúhelníku najdeme ALE 1 D:
Nyní vypočítáme objem pomocí vzorce (1):
Odpovědět: 192 cm3.
Příklad 3 Boční hrana pravidelného šestibokého hranolu je 14 cm. Plocha největší diagonální části je 168 cm 2. Najděte celkovou plochu hranolu.
Rozhodnutí. Udělejme nákres (obr. 4)

Největší diagonální řez je obdélník AA 1 DD 1, od úhlopříčky INZERÁT pravidelný šestiúhelník A B C D E F je největší. Aby bylo možné vypočítat boční povrch hranolu, je nutné znát stranu základny a délku bočního žebra.
Když známe plochu diagonální části (obdélník), najdeme úhlopříčku základny.
Od té doby ![]()
Od té doby AB= 6 cm.
Potom je obvod základny:
Najděte plochu bočního povrchu hranolu:
Plocha pravidelného šestiúhelníku o straně 6 cm je:
![]()
Najděte celkový povrch hranolu:
Odpovědět: ![]()
Příklad 4 Základem pravého rovnoběžnostěnu je kosočtverec. Plochy diagonálních sekcí jsou 300 cm2 a 875 cm2. Najděte oblast bočního povrchu rovnoběžnostěnu.
Rozhodnutí. Udělejme nákres (obr. 5).

Označte stranu kosočtverce pomocí A, úhlopříčky kosočtverce d 1 a d 2, výška krabice h. Chcete-li najít boční povrch rovného rovnoběžnostěnu, je nutné vynásobit obvod základny výškou: (vzorec (2)). Obvod základny p = AB + BC + CD + DA = 4AB = 4a, tak jako abeceda- kosočtverec. H = AA 1 = h. Že. Je potřeba najít A a h.
Zvažte diagonální řezy. AA 1 SS 1 - obdélník, jehož jedna strana je úhlopříčka kosočtverce AC = d 1, druhý boční okraj AA 1 = h, pak
Podobně pro oddíl BB 1 DD 1 dostaneme:
Pomocí vlastnosti rovnoběžníku takové, že součet čtverců úhlopříček je roven součtu čtverců všech jeho stran, dostaneme rovnost Dostaneme následující.
Různé hranoly se od sebe liší. Přitom mají hodně společného. Chcete-li najít oblast základny hranolu, musíte zjistit, jak vypadá.
Obecná teorie
Hranol je jakýkoli mnohostěn, jehož strany mají tvar rovnoběžníku. Kromě toho může být na své základně jakýkoli mnohostěn - od trojúhelníku po n-úhelník. Navíc jsou základny hranolu vždy stejné. Co neplatí pro boční plochy - mohou se výrazně lišit ve velikosti.
Při řešení problémů se nenarazí pouze na oblast základny hranolu. Může být nutné znát boční plochu, to znamená všechny plochy, které nejsou podstavy. Celá plocha již bude spojením všech tváří, které tvoří hranol.
Někdy se v úkolech objevují výšky. Je kolmá k základnám. Úhlopříčka mnohostěnu je segment, který v párech spojuje libovolné dva vrcholy, které nepatří do stejné plochy.
Je třeba poznamenat, že plocha základny rovného nebo šikmého hranolu nezávisí na úhlu mezi nimi a bočními plochami. Pokud mají stejné postavy v horní a dolní části, budou jejich plochy stejné.
trojboký hranol
Na základně má postavu se třemi vrcholy, tedy trojúhelník. Je známo, že je to jinak. Pokud pak stačí připomenout, že jeho plocha je určena polovičním součinem nohou.
Matematický zápis vypadá takto: S = ½ prům.
Chcete-li zjistit plochu základny v obecné podobě, jsou užitečné vzorce: Heron a ten, ve kterém je polovina strany vzata do výšky, která je k ní přikreslena.
První vzorec by měl být napsán takto: S \u003d √ (p (p-a) (p-in) (p-s)). Tato položka obsahuje semi-obvod (p), to znamená součet tří stran dělený dvěma.
Za druhé: S = ½ n a * a.
Pokud chcete znát plochu základny trojúhelníkového hranolu, která je pravidelná, pak je trojúhelník rovnostranný. Má svůj vlastní vzorec: S = ¼ a 2 * √3.

čtyřboký hranol
Jeho základna je některý ze známých čtyřúhelníků. Může to být obdélník nebo čtverec, rovnoběžnostěn nebo kosočtverec. V každém případě, abyste mohli vypočítat plochu základny hranolu, budete potřebovat svůj vlastní vzorec.
Pokud je základna obdélník, pak je jeho plocha určena následovně: S \u003d av, kde a, b jsou strany obdélníku.
Pokud jde o čtyřúhelníkový hranol, základní plocha pravidelného hranolu se vypočítá pomocí vzorce pro čtverec. Protože je to on, kdo leží na základně. S \u003d a 2.
V případě, že je základna rovnoběžnostěn, bude zapotřebí následující rovnost: S \u003d a * n a. Stává se, že je dána strana rovnoběžnostěnu a jeden z úhlů. Poté, abyste vypočítali výšku, budete muset použít další vzorec: na \u003d b * sin A. Navíc úhel A sousedí se stranou "b" a výška je proti tomuto úhlu.
Leží-li na základně hranolu kosočtverec, pak k určení jeho plochy bude potřeba stejný vzorec jako u rovnoběžníku (protože jde o jeho speciální případ). Ale můžete také použít toto: S = ½ d 1 d 2. Zde d 1 a d 2 jsou dvě úhlopříčky kosočtverce.

Pravidelný pětiboký hranol
V tomto případě jde o rozdělení mnohoúhelníku na trojúhelníky, jejichž oblasti lze snadněji zjistit. I když se stává, že obrazce mohou být s různým počtem vrcholů.
Protože základnou hranolu je pravidelný pětiúhelník, lze jej rozdělit na pět rovnostranných trojúhelníků. Pak se plocha základny hranolu rovná ploše jednoho takového trojúhelníku (vzorec je vidět výše), vynásobené pěti.

Pravidelný šestihranný hranol
Podle principu popsaného pro pětiboký hranol je možné rozdělit základní šestiúhelník na 6 rovnostranných trojúhelníků. Vzorec pro oblast základny takového hranolu je podobný předchozímu. Pouze v něm by mělo být vynásobeno šesti.
Vzorec bude vypadat takto: S = 3/2 a 2 * √3.

Úkoly
č. 1. Je dána pravidelná čára. Její úhlopříčka je 22 cm, výška mnohostěnu je 14 cm. Vypočítejte plochu základny hranolu a celého povrchu.
Rozhodnutí. Základna hranolu je čtverec, ale jeho strana není známa. Jeho hodnotu zjistíte z úhlopříčky čtverce (x), která souvisí s úhlopříčkou hranolu (d) a jeho výškou (h). x 2 \u003d d 2 - n 2. Na druhou stranu, tento segment "x" je přepona v trojúhelníku, jehož nohy se rovnají straně čtverce. To znamená, x 2 \u003d a 2 + a 2. Ukazuje se tedy, že a 2 \u003d (d 2 - n 2) / 2.
Nahraďte číslo 22 místo d a nahraďte „n“ jeho hodnotou - 14, ukázalo se, že strana čtverce je 12 cm. Nyní je snadné zjistit základní plochu: 12 * 12 \u003d 144 cm 2 .
Chcete-li zjistit plochu celého povrchu, musíte přidat dvojnásobek hodnoty základní plochy a zčtyřnásobit stranu. Ten lze snadno najít podle vzorce pro obdélník: vynásobte výšku mnohostěnu a stranu základny. To znamená, že 14 a 12, toto číslo se bude rovnat 168 cm2. Celková plocha hranolu je 960 cm 2 .
Odpovědět. Základní plocha hranolu je 144 cm2. Celá plocha - 960 cm 2 .
č. 2. Dana Na základně leží trojúhelník o straně 6 cm V tomto případě je úhlopříčka boční plochy 10 cm Vypočítejte plochy: základna a boční plocha.
Rozhodnutí. Protože je hranol pravidelný, jeho základna je rovnostranný trojúhelník. Jeho plocha se tedy rovná 6 čtvercům krát ¼ a druhé odmocnině 3. Jednoduchý výpočet vede k výsledku: 9√3 cm 2. Toto je oblast jedné základny hranolu.
Všechny boční plochy jsou stejné a jsou to obdélníky o stranách 6 a 10 cm, pro výpočet jejich ploch stačí tato čísla vynásobit. Pak je vynásobte třemi, protože hranol má přesně tolik bočních ploch. Poté se plocha boční plochy navine 180 cm 2 .
Odpovědět. Plochy: základna - 9√3 cm 2, boční plocha hranolu - 180 cm 2.