دورة محاضرة في الميكانيكا النظرية. ديناميات

كجزء من أي منهج دراسي ، تبدأ دراسة الفيزياء بالميكانيكا. ليس من الناحية النظرية ، وليس من التطبيقات وليس من الحسابات ، ولكن من الميكانيكا الكلاسيكية القديمة الجيدة. تسمى هذه الميكانيكا أيضًا ميكانيكا نيوتن. وفقًا للأسطورة ، كان العالم يسير في الحديقة ، ورأى سقوط تفاحة ، وكانت هذه الظاهرة هي التي دفعته إلى اكتشاف قانون الجاذبية الكونية. بالطبع ، كان القانون موجودًا دائمًا ، ولم يعطه نيوتن إلا شكلاً مفهومًا للناس ، لكن فائدته لا تقدر بثمن. في هذه المقالة ، لن نصف قوانين ميكانيكا نيوتن بأكبر قدر ممكن من التفاصيل ، لكننا سنحدد الأساسيات والمعرفة الأساسية والتعريفات والصيغ التي يمكن أن تلعبها دائمًا في يديك.

علم الميكانيكا هو فرع من فروع الفيزياء ، وهو علم يدرس حركة الأجسام المادية والتفاعلات بينها.

الكلمة نفسها من أصل يوناني وتُترجم على أنها "فن آلات البناء". لكن قبل بناء الآلات ، لا يزال أمامنا طريق طويل لنقطعه ، لذلك دعونا نتبع خطى أسلافنا ، وسوف ندرس حركة الحجارة التي تم رميها بزاوية مع الأفق ، وسقوط التفاح على الرؤوس من ارتفاع h.

لماذا تبدأ دراسة الفيزياء بالميكانيكا؟ لأنه أمر طبيعي تمامًا ألا نبدأ من توازن الديناميكا الحرارية ؟!

علم الميكانيكا من أقدم العلوم ، وتاريخيا بدأت دراسة الفيزياء على وجه التحديد مع أسس الميكانيكا. وبوضع الناس في إطار الزمان والمكان ، في الواقع ، لا يمكنهم البدء من شيء آخر ، مهما أرادوا ذلك. تحريك الأجساد هو أول ما ننتبه إليه.

ما هي الحركة؟

الحركة الميكانيكية هي تغيير في وضع الأجسام في الفضاء بالنسبة لبعضها البعض بمرور الوقت.

بعد هذا التعريف نصل بطبيعة الحال إلى مفهوم الإطار المرجعي. تغيير وضع الأجسام في الفضاء بالنسبة لبعضها البعض. الكلمات الدالةهنا: بالنسبة لبعضها البعض . بعد كل شيء ، يتحرك الراكب في السيارة بالنسبة لشخص يقف على جانب الطريق بسرعة معينة ، ويستريح بالنسبة لجاره في مقعد قريب ، ويتحرك بسرعة أخرى بالنسبة لراكب في السيارة التي يتفوق عليهم.

لهذا السبب ، من أجل قياس معلمات الأجسام المتحركة بشكل طبيعي وعدم الخلط ، نحتاج إلى ذلك نظام مرجعي - هيئة مرجعية مترابطة بشكل صارم ونظام تنسيق وساعة. على سبيل المثال ، تتحرك الأرض حول الشمس في إطار مرجعي مركزية الشمس. في الحياة اليومية ، نجري جميع قياساتنا تقريبًا في نظام مرجعي مركزية الأرض مرتبط بالأرض. الأرض هي جسم مرجعي بالنسبة إلى السيارات والطائرات والناس والحيوانات التي تتحرك.

الميكانيكا ، كعلم ، لها مهمتها الخاصة. مهمة الميكانيكا هي معرفة موضع الجسم في الفضاء في أي وقت. بعبارة أخرى ، تُنشئ الميكانيكا وصفًا رياضيًا للحركة وتجد صلات بين الكميات الفيزيائية التي تميزها.

من أجل المضي قدمًا ، نحتاج إلى فكرة " نقطة مادية ". يقولون أن الفيزياء علم دقيق ، لكن الفيزيائيين يعرفون كم عدد التقريبات والافتراضات التي يجب إجراؤها من أجل الاتفاق على هذه الدقة بالذات. لم يسبق لأحد أن رأى نقطة مادية أو شم غازًا مثاليًا ، لكنها موجودة! هم فقط أسهل بكثير للعيش معهم.

النقطة المادية هي الجسم الذي يمكن إهمال حجمه وشكله في سياق هذه المشكلة.

أقسام الميكانيكا الكلاسيكية

الميكانيكا تتكون من عدة أقسام

• معادلات الحركة
• ديناميات
• علم الإحصاء

معادلات الحركةمن وجهة نظر جسدية ، يدرس بالضبط كيف يتحرك الجسم. بمعنى آخر ، يتناول هذا القسم الخصائص الكمية للحركة. ابحث عن السرعة والمسار - المهام النموذجية للكينماتيكا

دينامياتيحل السؤال عن سبب تحركه بالطريقة التي يتحرك بها. أي أنها تعتبر القوى المؤثرة على الجسم.

علم الإحصاءيدرس توازن الأجسام تحت تأثير القوى ، أي أنه يجيب على السؤال: لماذا لا يسقط على الإطلاق؟

حدود تطبيق الميكانيكا الكلاسيكية

لم تعد الميكانيكا الكلاسيكية تدعي أنها علم يشرح كل شيء (في بداية القرن الماضي كان كل شيء مختلفًا تمامًا) ، ولديها نطاق واضح للتطبيق. بشكل عام ، فإن قوانين الميكانيكا الكلاسيكية صالحة للعالم المألوف لنا من حيث الحجم (macroworld). لقد توقفوا عن العمل في حالة عالم الجسيمات ، عندما يتم استبدال الميكانيكا الكلاسيكية بميكانيكا الكم. أيضًا ، الميكانيكا الكلاسيكية غير قابلة للتطبيق في الحالات التي تحدث فيها حركة الأجسام بسرعة قريبة من سرعة الضوء. في مثل هذه الحالات ، تصبح التأثيرات النسبية واضحة. بشكل تقريبي ، في إطار ميكانيكا الكم والنسبية - الميكانيكا الكلاسيكية ، هذه حالة خاصة عندما تكون أبعاد الجسم كبيرة والسرعة صغيرة.

بشكل عام ، لا تختفي التأثيرات الكمية والنسبية ؛ تحدث أيضًا أثناء الحركة المعتادة للأجسام العيانية بسرعة أقل بكثير من سرعة الضوء. شيء آخر هو أن تأثير هذه التأثيرات صغير جدًا بحيث لا يتجاوز القياسات الأكثر دقة. وهكذا لن تفقد الميكانيكا الكلاسيكية أهميتها الأساسية أبدًا.

سنواصل دراسة الأسس الفيزيائية للميكانيكا في المقالات المستقبلية. لفهم أفضل للميكانيكا ، يمكنك الرجوع دائمًا إلى مؤلفينا، والتي تسلط الضوء بشكل فردي على البقعة المظلمة من أصعب المهام.

شريحة واحدة

دورة محاضرات عن ميكانيكا نظريةديناميكيات (الجزء الأول) Bondarenko A.N. موسكو - 2007 تمت كتابة الدورة التدريبية الإلكترونية على أساس المحاضرات التي ألقاها المؤلف للطلاب الذين يدرسون في تخصصات SZhD و PGS و SDM في NIIZhT و MIIT (1974-2006). المواد التعليميةيتوافق خطط التقويمعلى مدى ثلاثة فصول دراسية. لتنفيذ تأثيرات الرسوم المتحركة بشكل كامل أثناء العرض التقديمي ، يجب عليك استخدام عارض Power Point ليس أقل من عارض Microsoft Office لنظام التشغيل Windows-XP Professional. يمكن إرسال التعليقات والاقتراحات عن طريق البريد الإلكتروني: [بريد إلكتروني محمي]. موسكو جامعة الدولةالسكك الحديدية (MIIT) قسم الميكانيكا النظرية المركز العلمي والتقني لتكنولوجيا النقل

2 شريحة

محاضرة المحتويات 1. مقدمة في الديناميات. قوانين وبديهيات ديناميكيات النقطة المادية. المعادلة الأساسية للديناميات. المعادلات التفاضلية والطبيعية للحركة. مهمتان رئيسيتان للديناميات. أمثلة على حل مشكلة الديناميكيات المباشرة. محاضرة 2. حل مشكلة الديناميكيات العكسية. تعليمات عامة لحل مشكلة الديناميكيات العكسية. أمثلة على حل المشكلة العكسية للديناميكيات. حركة جسم مُلقى بزاوية مع الأفق دون مراعاة مقاومة الهواء. المحاضرة 3. التذبذبات المستقيمة لنقطة مادية. شرط حدوث التذبذبات. تصنيف الاهتزازات. الاهتزازات الحرة دون مراعاة قوى المقاومة. الاهتزازات المخففة. تناقص التذبذب. المحاضرة 4. التذبذبات القسرية لنقطة مادية. صدى. تأثير مقاومة الحركة أثناء الاهتزازات القسرية. المحاضرة 5. الحركة النسبية لنقطة مادية. قوى الجمود. حالات خاصة للحركة لأنواع مختلفة من الحركة المحمولة. تأثير دوران الأرض على توازن وحركة الأجسام. المحاضرة 6. ديناميات النظام الميكانيكي. نظام ميكانيكي. القوى الخارجية والداخلية. مركز كتلة النظام. نظرية حركة مركز الكتلة. قوانين الحفظ. مثال على حل مشكلة استخدام النظرية في حركة مركز الكتلة. المحاضرة 7. دفعة القوة. مقدار الحركة. نظرية التغيير في الزخم. قوانين الحفظ. نظرية أويلر. مثال على حل المشكلة باستخدام نظرية التغيير في الزخم. لحظة الزخم. نظرية تغيير الزخم الزاوي محاضرة 8. قوانين الحفظ. عناصر نظرية لحظات القصور الذاتي. اللحظة الحركية لجسم صلب. معادلة تفاضلية لدوران جسم صلب. مثال لحل مشكلة استخدام النظرية في تغيير الزخم الزاوي للنظام. النظرية الأولية للجيروسكوب. الأدبيات الموصى بها 1. Yablonsky A.A. دورة الميكانيكا النظرية. الجزء 2. م: المدرسة العليا. 1977. 368 ص. 2. ميشيرسكي آي في. مجموعة من المشاكل في الميكانيكا النظرية. م: العلوم. 1986 416 ص. 3. مجموعة من المهام ل أوراق الفصل/ إد. أ. يابلونسكي. م: المدرسة العليا. 1985. 366 ص. 4 - بوندارينكو أ. "الميكانيكا النظرية في الأمثلة والمهام. Dynamics "(دليل إلكتروني www.miit.ru/institut/ipss/faculties/trm/main.htm) ، 2004

3 شريحة

المحاضرة 1 ديناميكيات هي قسم من الميكانيكا النظرية يدرس الحركة الميكانيكية من وجهة نظر عامة. تعتبر الحركة مرتبطة بالقوى المؤثرة على الجسم. يتكون القسم من ثلاثة أقسام: ديناميات نقطة مادة ديناميات نظام ميكانيكي ميكانيكا تحليلية ■ ديناميات نقطة - يدرس حركة نقطة مادة ، مع مراعاة القوى التي تسبب هذه الحركة. الهدف الرئيسي هو نقطة مادية - جسم مادي مع كتلة ، يمكن إهمال أبعادها. الافتراضات الأساسية: - هناك فضاء مطلق (له خصائص هندسية بحتة لا تعتمد على المادة وحركتها. - هناك زمن مطلق (لا يعتمد على المادة وحركتها) ويترتب على ذلك: - يوجد إطار مرجعي ثابت تمامًا. - الوقت لا يعتمد على حركة الإطار المرجعي. - لا تعتمد كتل النقاط المتحركة على حركة الإطار المرجعي.تستخدم هذه الافتراضات في الميكانيكا الكلاسيكية التي أنشأها جاليليو ونيوتن . لا يزال لها نطاق واسع إلى حد ما ، لأن الأنظمة الميكانيكية التي يتم النظر فيها في العلوم التطبيقية لا تحتوي على مثل هذه الكتل الكبيرة وسرعات الحركة ، والتي من الضروري أن تؤخذ في الاعتبار تأثيرها على هندسة المكان والزمان والحركة ، مثل تم إجراؤه في الميكانيكا النسبية (نظرية النسبية) ■ تشكل القوانين الأساسية للديناميكيات - التي اكتشفها جاليليو لأول مرة وصاغها نيوتن الأساس لجميع الطرق لوصف وتحليل حركة الأنظمة الميكانيكية وتفاعلها الديناميكي العمل تحت تأثير القوى المختلفة. ■ قانون القصور الذاتي (قانون جاليليو - نيوتن) - تحتفظ النقطة المادية المعزولة في الجسم بحالة الراحة أو الحركة المستقيمة المنتظمة حتى تجبرها القوى المطبقة على تغيير هذه الحالة. وهذا يعني تكافؤ حالة السكون والحركة بالقصور الذاتي (قانون النسبية لغاليليو). يُطلق على الإطار المرجعي ، فيما يتعلق بالوفاء بقانون القصور الذاتي ، بالقصور الذاتي. تسمى خاصية النقطة المادية التي تسعى جاهدة للحفاظ على سرعة حركتها (حالتها الحركية) دون تغيير بالقصور الذاتي. ■ قانون تناسب القوة والتسارع (المعادلة الأساسية للديناميكيات - قانون نيوتن الثاني) - التسارع الذي يتم نقله إلى نقطة مادية بالقوة يتناسب طرديًا مع القوة ويتناسب عكسيًا مع كتلة هذه النقطة: أو هنا m هو كتلة النقطة (مقياس القصور الذاتي) ، مقاسة بالكيلو جرام ، مساوية عدديًا للوزن مقسومًا على تسارع الجاذبية: F هي القوة المؤثرة ، مقاسة بـ N (1 N تضفي تسارعًا قدره 1 م / ث 2 إلى نقطة من الكتلة 1 كجم ، 1 N \ u003d 1/9. 81 كجم). ■ ديناميكيات النظام الميكانيكي - يدرس حركة مجموعة من النقاط المادية والأجسام الصلبة ، متحدة بقوانين التفاعل العامة ، مع مراعاة القوى التي تسبب هذه الحركة. ■ الميكانيكا التحليلية - يدرس حركة الأنظمة الميكانيكية غير الحرة باستخدام طرق التحليل العامة. واحد

4 شريحة

المحاضرة 1 (تتمة - 1.2) المعادلات التفاضليةحركة نقطة مادية: - معادلة تفاضلية لحركة نقطة في شكل متجه. - المعادلات التفاضلية لنقطة الحركة في شكل إحداثيات. يمكن الحصول على هذه النتيجة من خلال الإسقاط الرسمي للمعادلة التفاضلية المتجهة (1). بعد التجميع ، تتحلل علاقة المتجه إلى ثلاث معادلات عددية: في شكل إحداثيات: نستخدم علاقة متجه نصف القطر بالإحداثيات ومتجه القوة مع الإسقاطات: معادلة تفاضلية للحركة على محاور إحداثيات طبيعية (متحركة): أو: - المعادلات الطبيعية لحركة نقطة. ■ المعادلة الأساسية للديناميكيات: - تتوافق مع طريقة المتجه لتحديد حركة نقطة. ■ قانون استقلالية عمل القوى - يكون تسريع نقطة مادية تحت تأثير قوى متعددة مساويًا للمجموع الهندسي لتسارع نقطة من عمل كل قوة على حدة: أو القانون ساري المفعول لأية حالة حركية للأجسام. قوى التفاعل المطبقة على نقاط (أجسام) مختلفة ليست متوازنة. ■ قانون المساواة في الفعل ورد الفعل (قانون نيوتن الثالث) - كل فعل يتوافق مع رد فعل متساوٍ وموجه بشكل معاكس: 2

5 شريحة

مشكلتان رئيسيتان في الديناميات: 1. مشكلة مباشرة: تعطى الحركة (معادلات الحركة ، المسار). من الضروري تحديد القوى التي تحدث بموجبها حركة معينة. 2. المشكلة المعكوسة: يتم إعطاء القوى التي تحدث الحركة بموجبها. مطلوب للعثور على معلمات الحركة (معادلات الحركة ، مسار الحركة). يتم حل كلتا المشكلتين باستخدام المعادلة الأساسية للديناميكيات وإسقاطها على محاور الإحداثيات. إذا تم النظر في حركة النقطة غير الحرة ، عندئذٍ ، كما هو الحال في الإحصائيات ، يتم استخدام مبدأ التحرر من الروابط. نتيجة للتفاعل ، يتم تضمين الروابط في تكوين القوى المؤثرة على نقطة المادة. حل المشكلة الأولى مرتبط بعمليات التفاضل. يتطلب حل المسألة العكسية تكامل المعادلات التفاضلية المقابلة ، وهذا أصعب بكثير من التفاضل. المشكلة العكسية أصعب من المشكلة المباشرة. حل مشكلة الديناميكيات المباشرة - لنلق نظرة على أمثلة: مثال 1. حجرة بوزن G لمصعد يتم رفعها بواسطة كابل مع تسارع a. تحديد شد الكابل. 1. حدد شيئًا (تتحرك عربة المصعد للأمام ويمكن اعتبارها نقطة مادية). 2. نتجاهل الوصلة (الكبل) ونستبدلها بالتفاعل R. 3. كوّن المعادلة الأساسية للديناميكيات: حدد رد فعل الكبل: حدد شد الكبل: بحركة موحدة للكابينة ay = 0 و شد الكابل يساوي الوزن: T = G. عندما ينكسر الكابل T = 0 ويكون تسارع المقصورة مساويًا لتسارع السقوط الحر: ay = -g. 3 4. نقوم بإسقاط المعادلة الأساسية للديناميات على المحور y: y مثال 2. تتحرك نقطة الكتلة m على طول سطح أفقي (المستوى Oxy) وفقًا للمعادلات: x = a coskt ، y = b coskt. أوجد القوة المؤثرة على النقطة. 1. حدد كائنًا (نقطة مادية). 2. نتجاهل الوصلة (المستوي) ونستبدلها بالتفاعل N. 3. أضف قوة غير معروفة F إلى نظام القوى. 4. كوّن المعادلة الأساسية للديناميكيات: 5. اعرض المعادلة الأساسية للديناميكيات على المحاور س ، ص: تحديد إسقاط القوة: معامل القوة: جيب التمام للاتجاه: وبالتالي ، يتناسب حجم القوة مع مسافة النقطة إلى مركز الإحداثيات ويتجه نحو المركز على طول الخط الذي يربط النقطة بالمركز. مسار حركة النقطة هو شكل بيضاوي متمركز في الأصل: O r المحاضرة 1 (تابع - 1.3)

6 شريحة

المحاضرة 1 (تتمة 1.4) مثال 3: حمولة بوزن G معلقة على كابل طوله l وتتحرك على طول مسار دائري في مستوى أفقي بسرعة معينة. زاوية انحراف الكابل عن العمودي تساوي. حدد شد الكابل وسرعة الحمل. 1. حدد كائنًا (حمولة). 2. تجاهل الوصلة (الحبل) واستبدلها بالتفاعل R. 3. كوّن المعادلة الرئيسية للديناميكيات: من المعادلة الثالثة ، حدد رد فعل الكابل: حدد شد الكبل: استبدل قيمة التفاعل من الكبل ، التسارع الطبيعي في المعادلة الثانية وتحديد سرعة الحمل: 4. قم بإبراز ديناميكيات محور المعادلة الرئيسية ، n ، b: مثال 4: تتحرك سيارة وزنها G على جسر محدب (نصف قطر الانحناء هو R ) بالسرعة V. تحديد ضغط السيارة على الجسر. 1. نختار شيئًا (سيارة ، نهمل الأبعاد ونعتبرها نقطة). 2. نتجاهل الوصلة (السطح الخشن) ونستبدلها بالتفاعلات N وقوة الاحتكاك Ffr. 3. نؤلف المعادلة الأساسية للديناميكيات: 4. نضع المعادلة الأساسية للديناميكيات على المحور n: من هنا نحدد رد الفعل الطبيعي: نحدد ضغط السيارة على الجسر: من هنا يمكننا تحديد السرعة المقابلة للضغط الصفري على الجسر (س = 0): 4

7 شريحة

المحاضرة 2 بعد استبدال القيم الموجودة للثوابت ، نحصل على: وهكذا ، تحت تأثير نفس نظام القوى ، يمكن لنقطة مادية أن تؤدي فئة كاملة من الحركات التي تحددها الشروط الأولية. تأخذ الإحداثيات الأولية في الاعتبار الموضع الأولي للنقطة. تأخذ السرعة الأولية ، المعطاة من الإسقاطات ، في الحسبان التأثير على حركتها على طول المقطع المدروس لمسار القوى التي تصرفت في النقطة قبل الوصول إلى هذا القسم ، أي الحالة الحركية الأولية. حل المشكلة العكسية للديناميكيات - في الحالة العامة لحركة نقطة ، فإن القوى المؤثرة على النقطة هي متغيرات تعتمد على الوقت والإحداثيات والسرعة. يتم وصف حركة النقطة بنظام من ثلاث معادلات تفاضلية من الدرجة الثانية: بعد دمج كل منها ، سيكون هناك ستة ثوابت C1 ، C2 ، .... ، C6: قيم الثوابت C1 ، C2 ، ... . ، تم العثور على C6 من ستة شروط أولية عند t = 0: مثال 1 من حل المسألة العكسية: تتحرك نقطة مادة حرة كتلتها m تحت تأثير قوة F ، وهي ثابتة في الحجم والمقدار. . في اللحظة الأولى ، كانت سرعة النقطة v0 وتزامنت في اتجاه القوة. حدد معادلة حركة نقطة. 1. نؤلف المعادلة الأساسية للديناميكيات: 3. نخفض ترتيب المشتق: 2. نختار النظام المرجعي الديكارتي ، ونوجه المحور x على طول اتجاه القوة ونعرض المعادلة الرئيسية للديناميكيات على هذا المحور: أو xyz 4. افصل بين المتغيرات: 5. احسب التكاملات من كلا الجزأين من المعادلة: 6. دعنا نمثل إسقاط السرعة كمشتق زمني للإحداثيات: 8. احسب تكاملات كلا الجزأين من المعادلة: 7. افصل المتغيرات: 9. لتحديد قيم الثوابت C1 و C2 ، نستخدم الشروط الأولية t = 0 ، vx = v0 ، x = x0: نتيجة لذلك ، نحصل على معادلة الحركة المتغيرة المنتظمة (على طول المحور س): 5

8 شريحة

تعليمات عامة لحل المشاكل المباشرة والمعكوسة. إجراء الحل: 1. تجميع المعادلة التفاضلية للحركة: 1.1. اختر نظام إحداثيات - مستطيل (ثابت) مع مسار غير معروف للحركة ، طبيعي (متحرك) بمسار معروف ، على سبيل المثال ، دائرة أو خط مستقيم. في الحالة الأخيرة ، يمكن استخدام إحداثي مستقيم واحد. يجب دمج النقطة المرجعية مع الموضع الأولي للنقطة (عند t = 0) أو مع موضع توازن النقطة ، إذا كانت موجودة ، على سبيل المثال ، عندما تتقلب النقطة. 6 1.2. ارسم نقطة في موضع يقابل لحظة زمنية عشوائية (بالنسبة إلى t> 0) بحيث تكون الإحداثيات موجبة (s> 0 ، x> 0). نفترض أيضًا أن إسقاط السرعة في هذا الموضع موجب أيضًا. في حالة التذبذبات ، يتغير إسقاط السرعة ، على سبيل المثال ، عند العودة إلى وضع التوازن. هنا يجب أن نفترض أنه في اللحظة الزمنية المدروسة تتحرك النقطة بعيدًا عن موضع التوازن. تنفيذ هذه التوصية مهم في المستقبل عند العمل مع قوى المقاومة التي تعتمد على السرعة. 1.3 حرر نقطة المادة من الروابط ، واستبدل عملها بردود فعل ، وأضف قوى نشطة. 1.4 اكتب القانون الأساسي للديناميكيات في شكل متجه ، واسقط على محاور محددة ، وعبر عن القوى المعطاة أو التفاعلية من حيث الوقت أو الإحداثيات أو متغيرات السرعة ، إذا كانت تعتمد عليها. 2. حل المعادلات التفاضلية: 2.1. اختصر المشتق إذا لم يتم اختزال المعادلة إلى الشكل القياسي (القياسي). على سبيل المثال: أو 2.2. متغيرات منفصلة ، على سبيل المثال: أو 2.4. احسب التكاملات غير المحددة على الجانبين الأيمن والأيسر من المعادلة ، على سبيل المثال: 2.3. إذا كانت هناك ثلاثة متغيرات في المعادلة ، فقم بإجراء تغيير في المتغيرات ، على سبيل المثال: ثم افصل المتغيرات. تعليق. بدلا من الحساب تكاملات غير محددةمن الممكن حساب التكاملات المحددة بحد أعلى متغير. تمثل الحدود الدنيا القيم الأولية للمتغيرات (الشروط الأولية). ثم لا داعي لإيجاد الثابت بشكل منفصل ، والذي يتم تضمينه تلقائيًا في الحل ، على سبيل المثال: استخدام الشروط الأولية ، على سبيل المثال ، t = 0 ، vx = vx0 ، أوجد ثابت التكامل: 2.5. عبر عن السرعة من حيث مشتق التوقيت للإحداثيات ، على سبيل المثال ، وكرر الخطوتين 2.2 -2.4 ملاحظة. إذا تم تقليل المعادلة إلى شكل أساسي يحتوي على حل قياسي ، فسيتم استخدام هذا الحل الجاهز. لا تزال توجد ثوابت التكامل من الشروط الأولية. انظر ، على سبيل المثال ، التذبذبات (المحاضرة 4 ، ص 8). المحاضرة 2 (تتمة 2.2)

9 شريحة

المحاضرة 2 (تتمة 2.3) مثال 2 لحل المسألة العكسية: القوة تعتمد على الوقت. يبدأ حمل الوزن P بالتحرك على طول سطح أفقي أملس تحت تأثير القوة F ، يتناسب حجمها مع الوقت (F = kt). أوجد المسافة التي يقطعها الحمل في الزمن t. 3. قم بتكوين المعادلة الأساسية للديناميكيات: 5. تقليل ترتيب المشتق: 4. قم بإسقاط المعادلة الأساسية للديناميكيات على المحور x: أو 7 6. افصل بين المتغيرات: 7. احسب تكاملات كلا الجزأين من المعادلة: 9. مثل إسقاط السرعة كمشتق للإحداثيات بالنسبة للوقت: 10. احسب تكاملات كلا الجزأين من المعادلة: 9. افصل بين المتغيرات: 8. حدد قيمة الثابت C1 من الشرط الأولي t = 0 ، vx = v0 = 0: نتيجة لذلك ، نحصل على معادلة الحركة (على طول المحور x) ، والتي تعطي قيمة المسافة المقطوعة للوقت t: 1. نختار النظام المرجعي (الديكارتي) إحداثيات) بحيث يكون للجسم إحداثيات موجبة: 2. نأخذ الجسم المتحرك كنقطة مادية (يتحرك الجسم للأمام) ، ثم نحرره من الاتصال (المستوى المرجعي) ونستبدله بالتفاعل (رد الفعل الطبيعي لـ سطح أملس): 11. حدد قيمة الثابت C2 من الحالة الأولية t = 0 ، x = x0 = 0: مثال 3 لحل المسألة العكسية: تعتمد القوة على الإحداثي. تم طرح نقطة مادية كتلتها m لأعلى من سطح الأرض بسرعة v0. تتناسب قوة جاذبية الأرض عكسًا مع مربع المسافة من النقطة إلى مركز الجاذبية (مركز الأرض). أوجد اعتماد السرعة على المسافة ص إلى مركز الأرض. 1. نختار النظام المرجعي (الإحداثيات الديكارتية) بحيث يكون للجسم إحداثيات موجبة: 2. نؤلف المعادلة الأساسية للديناميكيات: 3. نعرض المعادلة الأساسية للديناميكيات على المحور y: أو يمكن لمعامل التناسب يمكن العثور عليها باستخدام وزن نقطة على سطح الأرض: R ومن هنا تبدو المعادلة كما يلي: أو 4. تصغير ترتيب المشتق: 5. قم بتغيير المتغير: 6. افصل بين المتغيرات: 7. احسب تكاملات طرفي المعادلة: 8. استبدل الحدود: نتيجة لذلك ، نحصل على تعبير للسرعة كدالة للإحداثي y: يمكن إيجاد أقصى ارتفاع للطيران من خلال معادلة السرعة بالصفر: أقصى ارتفاع للطيران عندما يتحول المقام إلى الصفر: من هنا ، عند تحديد نصف قطر الأرض وتسريع السقوط الحر ، يتم الحصول على السرعة الكونية الثانية:

10 شريحة

المحاضرة 2 (تتمة 2.4) مثال 2 لحل المسألة العكسية: تعتمد القوة على السرعة. كان لسفينة كتلتها m سرعة v0. تتناسب مقاومة الماء لحركة السفينة مع السرعة. حدد الوقت الذي تستغرقه سرعة السفينة لتنخفض بمقدار النصف بعد إيقاف تشغيل المحرك ، وكذلك المسافة التي تقطعها السفينة حتى التوقف التام. 8 1. نختار نظامًا مرجعيًا (الإحداثيات الديكارتية) بحيث يكون للجسم إحداثيات موجبة: 2. نأخذ موضوع الحركة كنقطة مادية (تتحرك السفينة للأمام) ، ونحرره من الروابط (الماء) ونستبدله مع رد فعل (قوة الطفو - قوة أرخميدس) ، وكذلك قوة مقاومة الحركة. 3. أضف القوة النشطة (الجاذبية). 4. نقوم بتكوين المعادلة الرئيسية للديناميكيات: 5. نقوم بإسقاط المعادلة الرئيسية للديناميكيات على المحور x: أو 6. نقوم بتخفيض ترتيب المشتق: 7. نقوم بفصل المتغيرات: 8. نحسب التكاملات من كليهما أجزاء من المعادلة: 9. نستبدل الحدود: يتم الحصول على تعبير يربط السرعة والوقت t ، والذي يمكنك من خلاله تحديد وقت الحركة: وقت الحركة ، حيث تنخفض السرعة خلاله بمقدار النصف: إنه من المثير للاهتمام ملاحظة أنه عندما تقترب السرعة من الصفر ، فإن وقت الحركة يميل إلى اللانهاية ، أي لا يمكن أن تكون السرعة النهائية صفرًا. لماذا لا تكون "الحركة الدائمة"؟ ومع ذلك ، في هذه الحالة ، فإن المسافة المقطوعة حتى نقطة التوقف هي قيمة محدودة. لتحديد المسافة المقطوعة ، ننتقل إلى التعبير الذي تم الحصول عليه بعد خفض ترتيب المشتق وإجراء تغيير في المتغير: بعد دمج الحدود واستبدالها ، نحصل على: المسافة المقطوعة إلى نقطة التوقف: ■ حركة نقطة تم إلقاؤها في زاوية إلى الأفق في مجال جاذبية منتظم دون مراعاة مقاومة الهواء. القضاء على الوقت من معادلات الحركة ، نحصل على معادلة المسار: يتم تحديد وقت الرحلة عن طريق معادلة الإحداثي y إلى الصفر: يتم تحديد نطاق الرحلة عن طريق استبدال وقت الرحلة:

11 شريحة

المحاضرة 3 التذبذبات المستقيمة الخطية لنقطة مادية - تحدث الحركة التذبذبية لنقطة مادية بشرط وجود قوة استعادة تميل إلى إرجاع النقطة إلى موضع التوازن لأي انحراف عن هذا الموضع. 9 هناك قوة استعادة ، وضع التوازن مستقر لا توجد قوة استعادة ، موضع التوازن غير مستقر لا توجد قوة استعادة ، موضع التوازن غير مبال يتم توجيهها دائمًا نحو وضع التوازن ، والقيمة تتناسب طرديًا مع الاستطالة الخطية (تقصير) الربيع ، مساوية لانحراف الجسم عن موضع التوازن: c هو معامل صلابة الزنبرك ، عدديًا متساوية في القوة، بموجب الإجراء الذي يغير الزنبرك طوله بمقدار واحد ، يقاس N / m في نظام SI. x y O أنواع اهتزازات النقطة المادية: 1. الاهتزازات الحرة (دون مراعاة مقاومة الوسط). 2. التذبذبات الحرة مع مراعاة مقاومة الوسط (التذبذبات المثبطة). 3. الاهتزازات القسرية. 4. التذبذبات القسرية مع مراعاة مقاومة الوسط. ■ التذبذبات الحرة - تحدث تحت تأثير قوة الاستعادة فقط. دعنا نكتب القانون الأساسي للديناميكيات: دعنا نختار نظام إحداثيات يتمحور حول موضع التوازن (النقطة O) ونعرض المعادلة على المحور x: لنجلب المعادلة الناتجة إلى النموذج القياسي (الأساسي): هذه المعادلة متجانسة معادلة تفاضلية خطية من الدرجة الثانية ، يتم تحديد شكل حلها من خلال جذور المعادلة المميزة التي تم الحصول عليها باستخدام الاستبدال الشامل: جذور المعادلة المميزة خيالية ومتساوية: الحل العام للمعادلة التفاضلية له الشكل: سرعة النقطة: الشروط الأولية: تحديد الثوابت: إذن ، المعادلة الاهتزازات الحرةلها الشكل: يمكن تمثيل المعادلة بتعبير من مصطلح واحد: حيث a هي السعة ، هي المرحلة الأولية. الثوابت الجديدة a و - مرتبطة بالثابتين C1 و C2 من خلال العلاقات: دعنا نحدد a و: سبب حدوث التذبذبات الحرة هو الإزاحة الأولية x0 و / أو السرعة الابتدائية v0.

12 شريحة

10 المحاضرة 3 (تتمة 3.2) التذبذبات الخافتة لنقطة مادية - تحدث الحركة التذبذبية لنقطة مادية في وجود قوة استعادة وقوة مقاومة للحركة. يتم تحديد اعتماد قوة المقاومة للحركة على الإزاحة أو السرعة من خلال الطبيعة المادية للوسيط أو الاتصال الذي يعيق الحركة. أبسط اعتماد هو الاعتماد الخطي على السرعة (المقاومة اللزجة): - معامل اللزوجة x y O المعادلة الأساسية للديناميكيات: إسقاط معادلة الديناميكيات على المحور: طريقة العرض القياسية: حيث يكون للمعادلة المميزة جذور: الحل العام لهذه المعادلة التفاضلية له شكل مختلف اعتمادًا على قيم الجذور: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >ك - حالة المقاومة عالية اللزوجة: - جذور حقيقية مختلفة. أو - هذه الوظائف غير دورية: 3. n = k: - الجذور حقيقية ومتعددة. هذه الوظائف هي أيضًا غير دورية:

13 شريحة

المحاضرة 3 (تتمة 3.3) تصنيف حلول التذبذبات الحرة. وصلات الربيع. صلابة مكافئة. y y 11 فرق. حرف المعادلة. جذر المعادلة char. المعادلة حل المعادلة التفاضلية الرسم البياني nk n = k

14 شريحة

المحاضرة 4 الاهتزازات الإجبارية لنقطة مادية - جنبًا إلى جنب مع قوة الاستعادة ، تعمل قوة متغيرة دوريًا ، تسمى القوة المضطربة. يمكن أن يكون للقوة المقلقة طبيعة مختلفة. على سبيل المثال ، في حالة معينة ، يؤدي التأثير القصور الذاتي للكتلة غير المتوازنة m1 لدوار دوار إلى إسقاطات القوة المتغيرة بشكل متناسق: المعادلة الرئيسية للديناميكيات: إسقاط معادلة الديناميكيات على المحور: لنجلب المعادلة إلى المعيار الشكل: 12 يتكون حل هذه المعادلة التفاضلية غير المتجانسة من جزأين x = x1 + x2: x1 هو الحل العام للمعادلة المتجانسة المقابلة و x2 هو حل خاص للمعادلة غير المتجانسة: نختار الحل المعين في شكل الجانب الأيمن: يجب تحقيق المساواة الناتجة لأي ر. ثم: أو هكذا ، مع العمل المتزامن لقوى الاستعادة والمزعجة ، تؤدي نقطة المادة حركة تذبذبية معقدة ، والتي تنتج عن إضافة (تراكب) الاهتزازات الحرة (x1) والقسرية (x2). إذا ص< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >ك (التذبذبات القسرية عالية التردد) ، فإن مرحلة التذبذبات تكون معاكسة لمرحلة القوة المزعجة:

15 شريحة

المحاضرة 4 (تتمة 4.2) 13 المعامل الديناميكي - نسبة اتساع التذبذبات القسرية إلى الانحراف الثابت لنقطة تحت تأثير قوة ثابتة H = const: اتساع التذبذبات القسرية: يمكن العثور على الانحراف الثابت من معادلة التوازن: هنا: ومن هنا: هكذا ، عند p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >ك (التردد العالي للتذبذبات القسرية) المعامل الديناميكي: الرنين - يحدث عندما يتزامن تواتر التذبذبات القسرية مع تواتر التذبذبات الطبيعية (ع = ك). يحدث هذا غالبًا عند بدء وإيقاف دوران الدوارات غير المتوازنة المثبتة على معلقات مرنة. المعادلة التفاضلية للتذبذبات ذات الترددات المتساوية: لا يمكن أخذ حل معين على شكل الجانب الأيمن ، لأن سيتم الحصول على حل يعتمد خطيًا (انظر الحل العام). الحل العام: استبدل في المعادلة التفاضلية: لنأخذ حلاً معينًا في الشكل ونحسب المشتقات: وهكذا ، يتم الحصول على الحل: أو التذبذبات القسرية عند الرنين لها سعة تزيد إلى أجل غير مسمى بما يتناسب مع الوقت. تأثير مقاومة الحركة أثناء الاهتزازات القسرية. المعادلة التفاضلية في وجود المقاومة اللزجة لها الشكل: يتم اختيار الحل العام من الجدول (المحاضرة 3 ، ص 11) اعتمادًا على نسبة n و k (انظر). نأخذ حلاً معينًا في الشكل ونحسب المشتقات: عوض في المعادلة التفاضلية: معادلة معاملات الدوال المثلثية المتطابقة ، نحصل على نظام من المعادلات: رفع المعادلتين إلى قوة وإضافةهما ، نحصل على سعة التذبذبات القسرية: بقسمة المعادلة الثانية على الأولى ، نحصل على انزياح الطور للتذبذبات القسرية: وهكذا ، فإن معادلة الحركة للتذبذبات القسرية ، مع مراعاة مقاومة الحركة ، على سبيل المثال ، لـ n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 شريحة

المحاضرة 5 الحركة النسبية لنقطة مادية - لنفترض أن نظام الإحداثيات المتحرك (غير القصور الذاتي) Oxyz يتحرك وفقًا لبعض القوانين المتعلقة بنظام الإحداثيات الثابت (بالقصور الذاتي) O1x1y1z1. حركة النقطة المادية M (x ، y ، z) بالنسبة للنظام المحمول Oxyz هي حركة نسبية ، بالنسبة إلى النظام غير المتحرك O1x1y1z1 مطلقة. حركة نظام Oxyz المحمول بالنسبة للنظام الثابت O1x1y1z1 هي حركة محمولة. 14 z x1 y1 z1 O1 xy M xyz O المعادلة الأساسية للديناميكيات: التسارع المطلق للنقطة: استبدل التسارع المطلق للنقطة في المعادلة الرئيسية للديناميكيات: لننقل المصطلحات مع تسريع الترجمة وكوريوليس إلى الجانب الأيمن: تحتوي المصطلحات المنقولة على أبعاد القوى وتُعتبر قوى القصور الذاتي المقابلة ، متساوية: ثم يمكن اعتبار الحركة النسبية للنقطة مطلقة إذا أضفنا القوى الانتقالية وقوى كوريوليس من القصور الذاتي إلى القوى المؤثرة: في الإسقاطات على المحاور في نظام الإحداثيات المتحرك ، لدينا: الدوران منتظم ، ثم e = 0: 2. حركة منحنية انتقالية: إذا كانت الحركة مستقيمة ، فعندئذ =: إذا كانت الحركة مستقيمة وموحدة ، فإن النظام المتحرك يكون بالقصور الذاتي والنسبي يمكن اعتبار الحركة مطلقة: لا توجد ظاهرة ميكانيكية يمكنها الكشف عن زي مستقيم مستقيم الحركة (مبدأ النسبية للميكانيكا الكلاسيكية). تأثير دوران الأرض على توازن الأجسام - لنفترض أن الجسم في حالة توازن على سطح الأرض عند خط عرض عشوائي φ (المتوازيات). تدور الأرض حول محورها من الغرب إلى الشرق بسرعة زاوية: يبلغ نصف قطر الأرض حوالي 6370 كم. S R هو التفاعل الكلي لسطح غير أملس. ز - قوة جذب الأرض إلى المركز. Ф - قوة الطرد المركزي من القصور الذاتي. حالة التوازن النسبي: ناتج قوى الجذب والقصور الذاتي هي قوة الجاذبية (الوزن): مقدار قوة الجاذبية (الوزن) على سطح الأرض هو P = mg. قوة الطرد المركزي للقصور الذاتي هي جزء صغير من قوة الجاذبية: إن انحراف قوة الجاذبية عن اتجاه قوة الجاذبية صغير أيضًا: وبالتالي ، يكون تأثير دوران الأرض على توازن الأجسام ضئيلًا للغاية ولا تؤخذ بعين الاعتبار في الحسابات العملية. الحد الأقصى لقيمة القوة بالقصور الذاتي (عند φ = 0 - عند خط الاستواء) هي 0.00343 فقط من قيمة الجاذبية

17 شريحة

المحاضرة 5 (تتمة 5.2) 15 تأثير دوران الأرض على حركة الأجسام في مجال جاذبية الأرض - لنفترض أن جسمًا يسقط على الأرض من ارتفاع معين H فوق سطح الأرض عند خط العرض φ. دعنا نختار إطارًا مرجعيًا متحركًا ، مرتبطًا بشكل صارم بالأرض ، موجهًا المحورين x و y بشكل عرضي إلى خط الطول والتوازي: معادلة الحركة النسبية: هنا ، يكون صغر قوة الطرد المركزي للقصور الذاتي مقارنة بقوة الجاذبية مأخوذ فى الإعتبار. وهكذا ، يتم تحديد قوة الجاذبية مع قوة الجاذبية. بالإضافة إلى ذلك ، نفترض أن الجاذبية موجهة بشكل عمودي على سطح الأرض بسبب صغر انحرافها ، كما نوقش أعلاه. تسارع كوريوليس يساوي المحور y باتجاه الغرب وموجهًا له. قوة كوريوليس القصور الذاتي موجهة في الاتجاه المعاكس. نتوقع معادلة الحركة النسبية على المحور: يعطي حل المعادلة الأولى: الشروط الأولية: يعطي حل المعادلة الثالثة: الشروط الأولية: تأخذ المعادلة الثالثة الشكل: الشروط الأولية: يعطي الحل: الحل الناتج يدل على أن الجسم ينحرف نحو الشرق عندما يسقط. دعونا نحسب قيمة هذا الانحراف ، على سبيل المثال ، عند السقوط من ارتفاع 100 متر.نجد وقت السقوط من حل المعادلة الثانية: وبالتالي ، فإن تأثير دوران الأرض على حركة الأجسام ضئيل للغاية للارتفاعات والسرعات العملية ولا تؤخذ في الاعتبار في الحسابات الفنية. يشير حل المعادلة الثانية أيضًا إلى وجود سرعة على طول المحور y ، والتي يجب أن تسبب أيضًا وتسبب التسارع المقابل وقوة كوريوليس القصور الذاتي. سيكون تأثير هذه السرعة وقوة القصور الذاتي المرتبطة بها على التغيير في الحركة أقل حتى من قوة قصور كوريوليس المرتبطة بالسرعة الرأسية.

18 شريحة

المحاضرة 6 ديناميات النظام الميكانيكي. نظام النقاط المادية أو النظام الميكانيكي - مجموعة من النقاط المادية أو تلك النقاط المادية التي توحدها القوانين العامة للتفاعل (يعتمد موضع أو حركة كل نقطة أو جسم على موضع وحركة جميع النقاط الأخرى) نظام النقاط الحرة - التي لا تقتصر حركتها على أي اتصالات (على سبيل المثال ، نظام كوكبي ، حيث تُعتبر الكواكب نقاطًا مادية). نظام النقاط غير الحرة أو النظام الميكانيكي غير الحر - حركة النقاط أو الأجسام المادية محدودة بالقيود المفروضة على النظام (على سبيل المثال ، آلية ، آلة ، إلخ). 16 قوى تعمل على النظام. بالإضافة إلى التصنيف الموجود سابقًا للقوى (القوى النشطة والمتفاعلة) ، تم تقديم تصنيف جديد للقوى: 1. القوى الخارجية (هـ) - التي تعمل على نقاط وأجسام النظام من نقاط أو هيئات ليست جزءًا من هذا النظام. 2. القوى الداخلية (1) - قوى التفاعل بين النقاط المادية أو الهيئات المدرجة في نظام معين. يمكن أن تكون نفس القوة قوة خارجية وداخلية. كل هذا يتوقف على أي نظام ميكانيكي يعتبر. على سبيل المثال: في نظام الشمس والأرض والقمر ، كل قوى الجاذبية بينهما داخلية. عند النظر إلى نظام الأرض والقمر ، تكون قوى الجاذبية المطبقة من جانب الشمس خارجية: CZL بناءً على قانون الفعل ورد الفعل ، كل قوة داخلية Fk تقابل قوة داخلية أخرى Fk '، متساوية في القيمة المطلقة ومعاكسة في اتجاه. يتبع ذلك خاصيتان رائعتان للقوى الداخلية: المتجه الرئيسي لجميع القوى الداخلية للنظام يساوي الصفر: اللحظة الرئيسية لجميع القوى الداخلية للنظام بالنسبة إلى أي مركز تساوي الصفر: أو في الإسقاطات على الإحداثيات المحاور: ملاحظة. على الرغم من أن هذه المعادلات تشبه معادلات التوازن ، إلا أنها ليست كذلك ، حيث يتم تطبيق القوى الداخلية على نقاط أو أجسام مختلفة في النظام ويمكن أن تتسبب في تحرك هذه النقاط (الأجسام) بالنسبة لبعضها البعض. ويترتب على هذه المعادلات أن القوى الداخلية لا تؤثر على حركة النظام ككل. مركز كتلة نظام النقاط المادية. لوصف حركة النظام ككل ، يتم إدخال نقطة هندسية ، تسمى مركز الكتلة ، يتم تحديد متجه نصف القطر من خلال التعبير ، حيث M هي كتلة النظام بأكمله: أو في الإسقاطات على الإحداثيات المحاور: صيغ مركز الكتلة مماثلة لتلك الخاصة بمركز الثقل. ومع ذلك ، فإن مفهوم مركز الكتلة أكثر عمومية ، لأنه لا يرتبط بقوى الجاذبية أو قوى الجاذبية.

19 شريحة

المحاضرة 6 (تتمة 6.2) 17 نظرية حول حركة مركز كتلة النظام - ضع في اعتبارك نظامًا من ن نقاط مادية. نقسم القوى المطبقة على كل نقطة إلى قوى خارجية وداخلية ونستبدلها بالنتيجة المقابلة Fke و Fki. دعنا نكتب لكل نقطة المعادلة الأساسية للديناميكيات: أو لنجمع هذه المعادلات على جميع النقاط: في الجانب الأيسر من المعادلة ، سنقدم الكتل تحت علامة المشتق ونستبدل مجموع المشتقات بالمشتق من المجموع: من تعريف مركز الكتلة: استبدل في المعادلة الناتجة: نحصل على أو: ناتج كتلة النظام وتسارع كتلة مركزه يساوي المتجه الرئيسي للقوى الخارجية. في الإسقاطات على محاور الإحداثيات: يتحرك مركز كتلة النظام كنقطة مادية مع كتلة تساوي كتلة النظام بأكمله ، حيث يتم تطبيق جميع القوى الخارجية المؤثرة على النظام. النتائج من النظرية على حركة مركز كتلة النظام (قوانين الحفظ): 1. إذا كان المتجه الرئيسي للقوى الخارجية للنظام في الفترة الزمنية صفرًا ، Re = 0 ، ثم سرعة المركز الكتلة ثابتة ، vC = const (يتحرك مركز الكتلة بشكل موحد في خط مستقيم - قانون حفظ مركز الحركة للكتلة). 2. إذا كان إسقاط المتجه الرئيسي للقوى الخارجية للنظام على المحور x في الفترة الزمنية يساوي صفرًا ، Rxe = 0 ، فإن سرعة مركز الكتلة على طول المحور x تكون ثابتة ، vCx = const (يتحرك مركز الكتلة بشكل موحد على طول المحور). عبارات مماثلة صحيحة بالنسبة لمحور y و z. مثال: يوجد شخصان كتلتهما m1 و m2 في قارب كتلته m3. في اللحظة الأولى ، كان القارب الذي كان يحمل أشخاصًا في حالة راحة. أوجد إزاحة القارب إذا تحرك شخص كتلته م 2 إلى قوس القارب على مسافة أ. 3. إذا كان المتجه الرئيسي للقوى الخارجية للنظام في الفترة الزمنية يساوي صفرًا ، Re = 0 ، وفي اللحظة الأولى كانت سرعة مركز الكتلة صفرًا ، vC = 0 ، فإن متجه نصف قطر يظل مركز الكتلة ثابتًا ، rC = const (مركز الكتلة في حالة سكون هو قانون الحفاظ على موضع مركز الكتلة). 4. إذا كان إسقاط المتجه الرئيسي للقوى الخارجية للنظام على المحور x في الفترة الزمنية يساوي صفرًا ، Rxe = 0 ، وفي اللحظة الأولى تكون سرعة مركز الكتلة على طول هذا المحور صفرًا ، vCx = 0 ، ثم يظل إحداثيات مركز الكتلة على طول المحور x ثابتًا ، xC = const (لا يتحرك مركز الكتلة على طول هذا المحور). عبارات مماثلة صحيحة بالنسبة لمحور y و z. 1. هدف الحركة (قارب به أشخاص): 2. نتجاهل الوصلات (الماء): 3. نستبدل الاتصال برد فعل: 4. أضف القوى النشطة: 5. اكتب النظرية حول مركز الكتلة: قم بالإسقاط على المحور x: O حدد المسافة التي تريد نقلها إلى شخص كتلته m1 ، بحيث يظل القارب في مكانه: سيتحرك القارب مسافة l في الاتجاه المعاكس.

20 شريحة

المحاضرة 7 نبضة القوة هي مقياس للتفاعل الميكانيكي الذي يميز انتقال الحركة الميكانيكية من القوى المؤثرة على نقطة لفترة زمنية معينة: 18 في الإسقاطات على محاور الإحداثيات: في حالة وجود قوة ثابتة: في الإسقاطات على محاور الإحداثيات: إلى نقطة القوة في نفس الفترة الزمنية: الضرب في dt: الدمج خلال فترة زمنية معينة: زخم النقطة هو مقياس للحركة الميكانيكية ، يتم تحديده بواسطة متجه يساوي منتج كتلة النقطة ومتجه السرعة الخاص بها: نظرية التغيير في زخم النظام - ضع في اعتبارك النظام n من النقاط المادية. نقسم القوى المطبقة على كل نقطة إلى قوى خارجية وداخلية ونستبدلها بالنتيجة المقابلة Fke و Fki. دعنا نكتب لكل نقطة المعادلة الأساسية للديناميات: أو كمية حركة نظام النقاط المادية - المجموع الهندسي لكميات حركة نقاط المواد: من خلال تعريف مركز الكتلة: متجه زخم النظام يساوي حاصل ضرب كتلة النظام بأكمله ومتجه السرعة لمركز كتلة النظام. ثم: في الإسقاطات على محاور الإحداثيات: المشتق الزمني لمتجه الزخم للنظام يساوي المتجه الرئيسي للقوى الخارجية للنظام. دعونا نجمع هذه المعادلات على جميع النقاط: في الجانب الأيسر من المعادلة ، نقدم الكتل تحت علامة المشتق ونستبدل مجموع المشتقات بمشتق المجموع: من تعريف زخم النظام: في الإسقاطات على محاور الإحداثيات:

21 شريحة

نظرية أويلر - تطبيق النظرية على التغيير في زخم النظام لحركة وسط مستمر (الماء). 1. نختار حجم الماء الموجود في القناة المنحنية للتوربينات كهدف للحركة: 2. نتجاهل الوصلات ونستبدل عملها بالتفاعلات (Rpov - الناتج عن قوى السطح) 3. أضف القوى النشطة (Rb - ناتج قوى الجسم): 4. اكتب النظرية حول التغيير في زخم النظام: سيتم تمثيل مقدار حركة الماء في الأوقات t0 و t1 كمجموع: التغيير في زخم الماء في الفترة الزمنية : التغيير في زخم الماء خلال فترة زمنية متناهية الصغر dt: ، حيث F1 F2 أخذ حاصل ضرب الكثافة ومساحة المقطع العرضي والسرعة لكل ثانية كتلة ، نحصل على: استبدال تفاضل زخم النظام في نظرية التغيير ، نحصل على: النتائج من النظرية على التغيير في زخم النظام (قوانين الحفظ): 1. إذا كان المتجه الرئيسي للقوى الخارجية للنظام في الفترة الزمنية يساوي صفرًا ، Re = 0 ، ثم حركة متجه الكمية ثابتة ، Q = const هي قانون الحفاظ على زخم النظام). 2. إذا كان إسقاط المتجه الرئيسي للقوى الخارجية للنظام على المحور x في الفترة الزمنية يساوي صفرًا ، Rxe = 0 ، فإن إسقاط زخم النظام على المحور x يكون ثابتًا ، Qx = const. عبارات مماثلة صحيحة بالنسبة لمحور y و z. المحاضرة 7 (تتمة 7.2) مثال: قنبلة يدوية كتلتها M ، تطير بسرعة v ، انفجرت إلى قسمين. زادت سرعة إحدى شظايا الكتلة m1 في اتجاه الحركة إلى القيمة v1. حدد سرعة الجزء الثاني. 1. موضوع الحركة (القنبلة): 2. الكائن هو نظام حر ، لا توجد وصلات وردود أفعالهم. 3. أضف القوى الفعالة: 4. اكتب النظرية حول التغيير في الزخم: المشروع على المحور: اقسم المتغيرات ودمج: التكامل الصحيح هو صفر تقريبًا ، لأن وقت الانفجار ر

22 شريحة

المحاضرة 7 (تتمة 7.3) 20 إن الزخم الزاوي لنقطة ما أو العزم الحركي للحركة بالنسبة إلى مركز معين هو مقياس للحركة الميكانيكية ، يتم تحديده بواسطة متجه يساوي منتج متجه لمتجه نصف القطر لنقطة مادية و متجه زخمها: إن اللحظة الحركية لنظام النقاط المادية بالنسبة إلى مركز معين هندسية مجموع لحظات عدد حركات جميع نقاط المواد بالنسبة إلى نفس المركز: في الإسقاطات على المحور: في الإسقاطات على المحور: نظرية التغيير في لحظة زخم النظام - ضع في اعتبارك نظامًا من ن نقاط مادية. نقسم القوى المطبقة على كل نقطة إلى قوى خارجية وداخلية ونستبدلها بالنتيجة المقابلة Fke و Fki. دعنا نكتب لكل نقطة المعادلة الأساسية للديناميكيات: أو لنجمع هذه المعادلات لجميع النقاط: دعنا نستبدل مجموع المشتقات بمشتق المجموع: التعبير بين قوسين هو لحظة زخم النظام. من هنا: نقوم بضرب كل من المساواة في متجه نصف القطر على اليسار: دعونا نرى ما إذا كان من الممكن أخذ علامة المشتق خارج حاصل الضرب المتجه: وهكذا ، حصلنا على: المركز. في الإسقاطات على محاور الإحداثيات: مشتق لحظة زخم النظام بالنسبة إلى بعض المحاور في الوقت المناسب يساوي اللحظة الرئيسية للقوى الخارجية للنظام بالنسبة إلى نفس المحور.

23 شريحة

المحاضرة 8 21 ■ النتائج المستمدة من النظرية على التغيير في الزخم الزاوي للنظام (قوانين الحفظ): 1. إذا كان متجه اللحظة الرئيسية للقوى الخارجية للنظام بالنسبة إلى مركز معين في الفاصل الزمني متساويًا إلى الصفر ، MO = 0 ، ثم يكون متجه الزخم الزاوي للنظام بالنسبة لنفس المركز ثابتًا ، KO = const هو قانون الحفاظ على زخم النظام). 2. إذا كانت اللحظة الرئيسية للقوى الخارجية للنظام بالنسبة للمحور x في الفترة الزمنية تساوي صفرًا ، Mxe = 0 ، فإن الزخم الزاوي للنظام بالنسبة إلى المحور x ثابت ، Kx = const. عبارات مماثلة صحيحة بالنسبة لمحور y و z. 2. لحظة القصور الذاتي لجسم صلب حول المحور: إن عزم القصور الذاتي لنقطة مادية حول المحور يساوي حاصل ضرب كتلة النقطة ومربع مسافة النقطة إلى المحور. تساوي لحظة القصور الذاتي لجسم صلب حول المحور مجموع حاصل ضرب كتلة كل نقطة ومربع مسافة هذه النقطة من المحور. ■ عناصر نظرية لحظات القصور الذاتي - مع الحركة الدورانية لجسم صلب ، فإن مقياس القصور الذاتي (مقاومة التغيير في الحركة) هو لحظة القصور الذاتي حول محور الدوران. ضع في اعتبارك المفاهيم الأساسية للتعريف وطرق حساب لحظات القصور الذاتي. 1. لحظة القصور الذاتي لنقطة مادية حول المحور: في الانتقال من كتلة صغيرة منفصلة إلى كتلة صغيرة غير محدودة من نقطة ما ، يتم تحديد حد هذا المجموع بالتكامل: عزم محوري من القصور الذاتي لجسم صلب . بالإضافة إلى العزم المحوري من القصور الذاتي للجسم الصلب ، هناك أنواع أخرى من لحظات القصور الذاتي: لحظة الطرد المركزي من القصور الذاتي للجسم الصلب. لحظة قطبية من القصور الذاتي لجسم صلب. 3. نظرية حول لحظات القصور الذاتي لجسم صلب حول محاور متوازية - صيغة الانتقال إلى محاور متوازية: لحظة من القصور الذاتي حول المحور المرجعي لحظات ثابتة من القصور الذاتي حول المحاور المرجعية كتلة الجسم المسافة بين المحورين z1 و z2 : اللحظات صفر:

24 شريحة

المحاضرة 8 (تتمة 8.2) 22 لحظة القصور الذاتي لقضيب منتظم ذي مقطع ثابت حول المحور: xz L حدد الحجم الأولي dV = Adx على مسافة x: x dx الكتلة الأولية: لحساب لحظة القصور الذاتي حول المحور المركزي (بالمرور عبر مركز الثقل) ، يكفي تغيير موقع المحور وضبط حدود التكامل (-L / 2 ، L / 2). نوضح هنا صيغة الانتقال إلى المحاور المتوازية: zС 5. لحظة القصور الذاتي لأسطوانة صلبة متجانسة حول محور التناظر: H dr r دعونا نفرد الحجم الأولي dV = 2πrdrH (أسطوانة رفيعة نصف قطرها r) : الكتلة الأولية: هنا نستخدم صيغة حجم الأسطوانة V = πR2H. لحساب عزم القصور الذاتي لأسطوانة مجوفة (سميكة) ، يكفي تعيين حدود التكامل من R1 إلى R2 (R2> R1): 6. لحظة القصور الذاتي لأسطوانة رقيقة حول محور التناظر (t

25 شريحة

المحاضرة 8 (تتمة 8.3) 23 ■ المعادلة التفاضلية لدوران جسم صلب حول محور: لنكتب نظرية حول تغيير الزخم الزاوي لجسم صلب يدور حول محور ثابت: زخم جسم صلب دوار هو: اللحظة القوى الخارجية حول محور الدوران تساوي عزم الدوران (التفاعلات والقوة لا تخلق لحظات الجاذبية): نستبدل العزم الحركية وعزم الدوران في النظرية مثال: شخصان لهما نفس الوزن G1 = G2 معلقان على حبل تم إلقاؤه فوق كتلة صلبة بوزن G3 = G1 / 4. في مرحلة ما ، بدأ أحدهم في تسلق الحبل بسرعة نسبية u. حدد سرعة الرفع لكل شخص. 1. حدد هدف الحركة (منع مع الأشخاص): 2. تجاهل التوصيلات (الجهاز الداعم للكتلة): 3. استبدل الاتصال بردود الفعل (تحمل): 4. أضف قوى نشطة (الجاذبية): 5. اكتب النظرية حول تغيير اللحظة الحركية للنظام فيما يتعلق بمحور دوران الكتلة: R نظرًا لأن لحظة القوى الخارجية تساوي الصفر ، يجب أن تظل العزم الحركية ثابتة: في اللحظة الأولى من الزمن t = 0 ، هناك كان التوازن و Kz0 = 0. بعد بداية حركة شخص واحد بالنسبة للحبل ، بدأ النظام بأكمله في التحرك ، ولكن يجب أن تظل العزم الحركية للنظام مساوية للصفر: Kz = 0. الزخم الزاوي للحبل النظام هو مجموع الزخم الزاوي لكل من الأشخاص والكتلة: هنا v2 هي سرعة الشخص الثاني ، مساوية لسرعة الكابل ، مثال: تحديد فترة التذبذبات الحرة الصغيرة لقضيب متجانس كتلته M و الطول l ، معلقًا بنهاية واحدة لمحور دوران ثابت. أو: في حالة التذبذبات الصغيرة sinφ φ: فترة التذبذب: لحظة القصور الذاتي للشريط:

26 شريحة

المحاضرة 8 (تتمة 8.4 - مادة إضافية) 24 ■ النظرية الأولية للجيروسكوب: الجيروسكوب عبارة عن جسم صلب يدور حول محور تناظر المادة ، إحدى نقاطه ثابتة. يتم إصلاح الجيروسكوب الحر بحيث يظل مركز كتلته ثابتًا ، ويمر محور الدوران عبر مركز الكتلة ويمكن أن يتخذ أي موضع في الفضاء ، أي يغير محور الدوران موضعه مثل محور دوران الجسم أثناء الحركة الكروية. الافتراض الرئيسي للنظرية التقريبية (الأولية) للجيروسكوب هو أن ناقل الزخم (العزم الحركي) للدوار يعتبر موجهًا على طول محور الدوران الخاص به. وهكذا ، على الرغم من حقيقة أن الجزء المتحرك في الحالة العامة يشارك في ثلاث دورات ، يتم أخذ السرعة الزاوية لدورانه فقط ω = dφ / dt في الاعتبار. أساس هذا هو أنه في التقنية الحديثةيدور دوار الجيروسكوب بسرعة زاوية تتراوح من 5000-8000 راد / ثانية (حوالي 50000-80000 دورة في الدقيقة) ، بينما السرعتان الزاويتان الأخريان المرتبطة بالدوران المسبق وتحريك محور الدوران الخاص به هما عشرات الآلاف من المرات أقل من هذه السرعة. الخاصية الرئيسية للجيروسكوب الحر هي أن محور الدوار يحافظ على نفس الاتجاه في الفضاء فيما يتعلق بالنظام المرجعي بالقصور الذاتي (النجمي) (تم توضيحه بواسطة بندول فوكو ، الذي يحافظ على مستوى التأرجح دون تغيير بالنسبة للنجوم ، 1852). هذا يتبع من قانون الحفاظ على اللحظة الحركية بالنسبة لمركز كتلة الدوار ، بشرط أن يتم إهمال الاحتكاك في محامل محاور التعليق الدوار ، والإطار الخارجي والداخلي: جيروسكوب. في حالة القوة المطبقة على محور الدوار ، فإن لحظة القوى الخارجية بالنسبة لمركز الكتلة لا تساوي الصفر: ω ω С ، وباتجاه متجه لحظة هذه القوة ، أي لن يدور حول المحور السيني (التعليق الداخلي) ، ولكن حول المحور الصادي (التعليق الخارجي). عند إنهاء القوة ، سيبقى محور الدوار في نفس الموضع ، بما يتوافق مع آخر وقت للقوة ، لأن من هذه النقطة الزمنية ، تصبح لحظة القوى الخارجية مرة أخرى مساوية للصفر. في حالة تأثير (تأثير) القوة قصير المدى ، فإن محور الجيروسكوب عمليًا لا يغير موضعه. وبالتالي ، فإن الدوران السريع للدوار يمنح الجيروسكوب القدرة على مواجهة التأثيرات العشوائية التي تميل إلى تغيير موضع محور دوران الدوار ، ومع العمل المستمر للقوة ، فإنه يحافظ على موضع المستوى المتعامد مع قوة التشغيلالذي يحتوي على محور الدوار. تستخدم هذه الخصائص في تشغيل أنظمة الملاحة بالقصور الذاتي.

رأي:تمت قراءة هذه المقالة 32852 مرة

Pdf حدد اللغة ... الروسية الإنجليزية الأوكرانية

مراجعة قصيرة

يتم تنزيل المواد الكاملة أعلاه ، بعد اختيار اللغة

• علم الإحصاء
  • المفاهيم الأساسية للإحصاء
  • أنواع القوة
  • البديهيات الاستاتيكية
  • الروابط وردود أفعالهم
  • نظام القوة المتقاربة
    • طرق تحديد النظام الناتج للقوى المتقاربة
    • شروط التوازن لنظام القوى المتقاربة
  • لحظة القوة حول المركز كمتجه
    • القيمة الجبرية لعزم القوة
    • خصائص لحظة القوة حول المركز (نقطة)
  • نظرية أزواج القوى
    • جمع قوتين متوازيتين في نفس الاتجاه
    • إضافة قوتين متوازيتين موجهتين في اتجاهين متعاكسين
    • أزواج القوة
    • زوجان من نظريات القوى
    • شروط لتوازن نظام من أزواج القوى
  • ذراع الرافعة
  • نظام القوات التعسفي
    • حالات تقليل نظام القوى المسطح إلى شكل أبسط
    • شروط التوازن التحليلي
  • مركز القوى الموازية. مركز الجاذبية
    • مركز القوى الموازية
    • مركز الثقل لجسم صلب وإحداثياته
    • مركز ثقل الحجم والمستويات والخطوط
    • طرق تحديد موقع مركز الثقل
• أساسيات مضارب القوة
  • مشاكل وطرق مقاومة المواد
  • تصنيف الحمل
  • تصنيف العناصر الإنشائية
  • تشوهات القضيب
  • الفرضيات والمبادئ الرئيسية
  • القوى الداخلية. طريقة القسم
  • الجهد االكهربى
  • التوتر والضغط
  • الخصائص الميكانيكية للمادة
  • الضغوط المسموح بها
  • صلابة المواد
  • قطع من القوى والضغوط الطولية
  • يحول
  • الخصائص الهندسية للأقسام
  • التواء
  • يلوي
    • التبعيات التفاضلية في الانحناء
    • قوة العاطفة
    • ضغوط طبيعية. حساب القوة
    • إجهادات القص في الانحناء
    • الانحناء صلابة
  • عناصر النظرية العامة لحالة الإجهاد
  • نظريات القوة
  • الانحناء مع تطور
• معادلات الحركة
  • حركيات النقطة
    • مسار النقطة
    • طرق تحديد حركة نقطة
    • سرعة النقطة
    • تسريع النقطة
  • حركيات الجسم الصلبة
    • حركة انتقالية لجسم صلب
    • الحركة الدورانية لجسم صلب
    • حركية آليات التروس
    • حركة موازية للمستوى لجسم صلب
  • حركة النقطة المعقدة
• ديناميات
  • القوانين الأساسية للديناميات
  • ديناميات النقطة
    • المعادلات التفاضلية لنقطة مادية حرة
    • مشكلتان لديناميكيات النقطة
  • ديناميكيات الجسم الصلبة
    • تصنيف القوى التي تعمل على نظام ميكانيكي
    • المعادلات التفاضلية للحركة لنظام ميكانيكي
  • النظريات العامة للديناميات
    • نظرية حول حركة مركز كتلة النظام الميكانيكي
    • نظرية التغيير في الزخم
    • نظرية التغيير في الزخم الزاوي
    • نظرية تغيير الطاقة الحركية
• القوى العاملة في الآلات
  • القوات في الاشتباك مع أداة دفع
  • الاحتكاك في الآليات والآلات
    • انزلاق الاحتكاك
    • الاحتكاك المتداول
  • كفاءة
• أجزاء الآلة
  • الإرسال الميكانيكي
    • أنواع التروس الميكانيكية
    • البارامترات الأساسية والمشتقة للتروس الميكانيكية
    • التروس
    • التروس ذات الروابط المرنة
  • مهاوي
    • الغرض والتصنيف
    • حساب التصميم
    • تحقق من حساب الأعمدة
  • رمان
    • محامل عادي
    • المتداول محامل
  • توصيل أجزاء الآلة
    • أنواع الوصلات القابلة للفصل والدائمة
    • اتصالات مقفولة
• توحيد المعايير ، التبادلية
  • التسامح والهبوط
  • النظام الموحد للتفاوتات والإنزال (ESDP)
  • انحراف الشكل والموقف

التنسيق: pdf

الحجم: 4 ميجابايت

اللغة الروسية

مثال على حساب ترس حفز
مثال على حساب ترس حفز. تم تنفيذ اختيار المواد وحساب الضغوط المسموح بها وحساب التلامس وقوة الانحناء.

مثال على حل مشكلة ثني العارضة
في المثال ، يتم رسم المخططات للقوى العرضية ولحظات الانحناء ، ويتم العثور على قسم خطير ، ويتم تحديد شعاع I. في المشكلة ، تم تحليل بناء المخططات باستخدام التبعيات التفاضلية ، وتحليل مقارن لمختلف المقاطع العرضيةأشعة.

مثال على حل مشكلة التواء العمود
وتتمثل المهمة في اختبار قوة العمود الفولاذي لقطر معين ومادة وضغوط مسموح بها. أثناء الحل ، يتم إنشاء مخططات عزم الدوران وضغوط القص وزوايا الالتواء. لا يؤخذ الوزن الذاتي للعمود في الاعتبار

مثال على حل مشكلة ضغط الشد لقضيب
وتتمثل المهمة في اختبار قوة قضيب فولاذي عند ضغوط معينة مسموح بها. أثناء الحل ، يتم إنشاء قطع من القوى الطولية والضغوط والتهجير الطبيعي. لا يتم أخذ الوزن الذاتي للشريط في الاعتبار

تطبيق نظرية حفظ الطاقة الحركية
مثال لحل مشكلة تطبيق النظرية على حفظ الطاقة الحركية لنظام ميكانيكي

تحديد سرعة نقطة ما وتسارعها وفقًا لمعادلات الحركة المعطاة
مثال لحل مشكلة تحديد سرعة وتسارع نقطة ما وفقًا لمعادلات الحركة المعطاة

تحديد سرعات وتسارعات نقاط جسم صلب أثناء الحركة الموازية للمستوى
مثال لحل مشكلة تحديد سرعات وتسارعات نقاط جسم صلب أثناء الحركة المتوازية للمستوى

تحديد القوى في قضبان الجمالون المستوية
مثال على حل مشكلة تحديد القوى في قضبان الجمالون المسطح بطريقة ريتر وطريقة قطع العقدة

مؤسسة الدولة المستقلة

منطقة كالينينغراد

المحترفين منظمة تعليمية

كلية الخدمة والسياحة

دورة محاضرات مع أمثلة للمهام العملية

"أساسيات الميكانيكا النظرية"

عن طريق الانضباطميكانيكا فنية

للطلاب3 مسار

تخصص20.02.04 السلامة من الحرائق

كالينينغراد

يوافق

نائب مدير SD GAU KO VEO KSTN.N. مياسنيكوف

وافق

المجلس المنهجي لـ GAU KO VET KST

اعتبر

في اجتماع PCC

فريق التحرير:

Kolganova AA ، المنهجي

Falaleeva AB ، مدرس اللغة الروسية وآدابها

Tsvetaeva L.V. ، رئيس PCCالتخصصات العامة في الرياضيات والطبيعية

جمعتها:

Nezvanova I.V. محاضر GAU KO VET KST

محتوى

1. المعلومات النظرية

1. المعلومات النظرية

1. أمثلة على حل المشكلات العملية

الديناميات: المفاهيم الأساسية والبديهيات

1. المعلومات النظرية

1. أمثلة على حل المشكلات العملية

فهرس

الإحصائيات: المفاهيم الأساسية والبديهيات.

1. المعلومات النظرية

علم الإحصاء - قسم من الميكانيكا النظرية ، يدرس خصائص القوى المطبقة على نقاط الجسم الصلب ، وظروف توازنها. المهام الرئيسية:

1. تحويل أنظمة القوات إلى أنظمة قوى متكافئة.

2. تحديد شروط توازن أنظمة القوى المؤثرة على جسم صلب.

نقطة مادية يسمى أبسط نموذج لجسم مادي

أي شكل ، أبعاده صغيرة بما يكفي ويمكن اعتباره نقطة هندسية لها كتلة معينة. النظام الميكانيكي هو أي مجموعة من النقاط المادية. الجسم الصلب تمامًا هو نظام ميكانيكي ، لا تتغير المسافات بين نقطتيه تحت أي تفاعلات.

الخضوع ل هو مقياس للتفاعل الميكانيكي للأجسام المادية مع بعضها البعض. القوة هي كمية متجهة ، حيث يتم تحديدها من خلال ثلاثة عناصر:

قيمة عددية

اتجاه؛

نقطة التطبيق (أ).

وحدة القوة هي نيوتن (N).

الشكل 1.1

نظام القوى هو مجموعة من القوى التي تعمل على الجسم.

نظام القوى المتوازن (الذي يساوي الصفر) هو نظام لا يغير حالته عند تطبيقه على الجسم.

يمكن استبدال نظام القوى المؤثرة على الجسم بمحصلة واحدة تعمل كنظام قوى.

البديهيات الاستاتيكية.

اكسيوم 1: إذا تم تطبيق نظام متوازن من القوى على الجسم ، فإنه يتحرك بشكل موحد ومستقيم أو في حالة سكون (قانون القصور الذاتي).

اكسيوم 2: يكون الجسم الصلب تمامًا في حالة توازن تحت تأثير قوتين إذا وفقط إذا كانت هذه القوى متساوية في القيمة المطلقة ، تعمل في خط مستقيم واحد ويتم توجيهها في اتجاهين متعاكسين. الشكل 1.2

اكسيوم 3: لن يتم إزعاج الحالة الميكانيكية للجسم إذا تمت إضافة نظام متوازن من القوى إلى نظام القوى المؤثرة عليه أو طرحه منه.

اكسيوم 4: نتيجة القوتين المطبقة على الجسم تساوي مجموعها الهندسي ، أي يتم التعبير عنها بالقيمة المطلقة والاتجاه بقطر متوازي الأضلاع المبني على هذه القوى كما هو الحال على الجانبين.

الشكل 1.3.

اكسيوم 5: دائمًا ما تكون القوى التي يعمل بها جسمان على بعضهما البعض متساوية في القيمة المطلقة وموجهة على طول خط مستقيم واحد في اتجاهين متعاكسين.

الشكل 1.4.

أنواع الروابط وردود أفعالها

روابط تسمى أي قيود تمنع حركة الجسم في الفضاء. الجسم ، الذي يسعى تحت تأثير القوى المطبقة للتحرك ، والذي يمنعه الاتصال ، سوف يعمل عليه بقوة معينة تسمى قوة الضغط على الاتصال . وفقًا لقانون المساواة في الفعل ورد الفعل ، سيعمل الاتصال على الجسم بنفس المعامل ، لكن القوة الموجهة بشكل معاكس.
تسمى القوة التي يعمل بها هذا الاتصال على الجسم ، والتي تمنع حركة أو أخرى قوة رد الفعل (رد فعل) الرابطة .
أحد المبادئ الأساسية للميكانيكا هو مبدأ التحرير : يمكن اعتبار أي جسم غير حر حرًا ، إذا تخلصنا من الروابط واستبدلنا عملها بردود فعل الروابط.

يتم توجيه تفاعل الرابطة في الاتجاه المعاكس حيث لا تسمح الرابطة للجسم بالتحرك. يتم عرض الأنواع الرئيسية للروابط وردود فعلها في الجدول 1.1.

الجدول 1.1

أنواع الروابط وردود أفعالها

اسم الاتصال

رمز

1

سطح أملس (دعم) - السطح (الدعم) ، الاحتكاك الذي يمكن أن يُهمل فيه الجسم المعطى.
مع الدعم المجاني ، رد الفعليتم توجيهه عموديًا على المماس عبر النقطةلكن هيئة الاتصالات1 مع سطح الدعم2 .

2

الخيط (مرن ، غير قابل للتمدد). الاتصال ، المصنوع على شكل خيط غير مرن ، لا يسمح للجسم بالابتعاد عن نقطة التعليق. لذلك ، يتم توجيه رد فعل الخيط على طول الخيط إلى نقطة تعليقه.

3

قضيب عديم الوزن - قضيب يمكن إهمال وزنه مقارنة بالحمل المدرك.
يتم توجيه رد فعل قضيب مستقيم مستقيم مفصلي عديم الوزن على طول محور القضيب.

4

مفصلة متحركة ، دعم متحرك مفصلي. يتم توجيه التفاعل على طول السطح الطبيعي إلى السطح الداعم.

7

إغلاق صارم. في مستوى التضمين الصلب ، سيكون هناك مكونان للتفاعل, ولحظة زوج من القوى، مما يمنع الشعاع من الدوران1 نسبة إلى هذه النقطةلكن .
يسلب التعلق الصلب في الفضاء جميع درجات الحرية الست من الجسم 1 - ثلاثة إزاحات على طول محاور الإحداثيات وثلاث دورات حول هذه المحاور.
سيكون هناك ثلاثة مكونات في التضمين المكاني الصلب, , وثلاث لحظات من أزواج القوات.

نظام القوة المتقاربة

نظام القوى المتقاربة يسمى نظام القوى الذي تتقاطع خطوط عمله عند نقطة واحدة. قوتان تتقاربان عند نقطة واحدة ، وفقًا للبديهية الثالثة للإحصاءات ، يمكن استبدالها بقوة واحدة -الناتج .
الموجه الرئيسي لنظام القوات - قيمة تساوي المجموع الهندسي لقوى النظام.

نتيجة لنظام مستوي من القوى المتقاربة يمكن تحديدهبيانيا و تحليليا.

إضافة نظام القوات . تتم إضافة نظام مسطح للقوى المتقاربة إما عن طريق الجمع المتتالي للقوى مع بناء نتيجة وسيطة (الشكل 1.5) ، أو ببناء مضلع قوة (الشكل 1.6).

الشكل 1.5 الشكل 1.6

إسقاط القوة على المحور - كمية جبرية تساوي حاصل ضرب مقياس القوة وجيب تمام الزاوية بين القوة والاتجاه الموجب للمحور.
تنبؤFx(الشكل 1.7) القوى لكل محور Xموجب إذا كانت α حادة ، وسلبية إذا كانت α منفرجة. إذا كانت القوةعمودي على المحور ، فإن إسقاطه على المحور يساوي صفرًا.

الشكل 1.7

إسقاط القوة على الطائرة أوهو- المتجه ، واختتم بين توقعات بداية القوة ونهايتهالهذه الطائرة. أولئك. إن إسقاط القوة على المستوى هو كمية متجهة ، لا تتميز فقط بقيمة عددية ، ولكن أيضًا بالاتجاه في المستوىأوهو (الشكل 1.8).

الشكل 1.8

ثم وحدة الإسقاطالى الطائرة أوهو ستكون مساوية لـ:

Fس ص = F.كوسلفا

حيث α هي الزاوية بين اتجاه القوةوإسقاطها.
طريقة تحليلية لتحديد القوى . للطريقة التحليلية لتحديد القوةمن الضروري اختيار نظام محاور الإحداثياتأوه، فيما يتعلق به سيتم تحديد اتجاه القوة في الفضاء.
ناقلات تصور القوة، يمكن بناؤها إذا كان معامل هذه القوة والزوايا α ، β ، التي تشكلها القوة مع محاور الإحداثيات معروفة. نقطةلكنتطبيق القوة يتم تعيينها بشكل منفصل بواسطة إحداثياتهاX, في, ض. يمكنك ضبط القوة من خلال توقعاتهاfx, السنة المالية, معلى محاور الإحداثيات. يتم تحديد معامل القوة في هذه الحالة بالصيغة:

وجيب التمام للاتجاه:

, .

طريقة تحليلية لإضافة القوى : إن إسقاط متجه المجموع على بعض المحاور يساوي المجموع الجبري لإسقاطات شروط المتجهات على نفس المحور ، أي إذا:

ومن بعد ، ، .
معرفة Rx ، Ry ، Rz، يمكننا تحديد الوحدة

وجيب التمام للاتجاه:

, , .

الشكل 1.9

تم إغلاقه (نهاية متجه المصطلح الأخير

يجب أن تتزامن القوة مع بداية متجه المصطلح الأول للقوة). ثم سيكون المتجه الرئيسي لنظام القوى يساوي صفرًا ()
2) شروط التوازن التحليلي . يتم تحديد وحدة المتجه الرئيسي لنظام القوات من خلال الصيغة. = 0. بقدر ما ، إذن يمكن أن يكون التعبير الجذر مساويًا للصفر فقط إذا اختفى كل مصطلح في نفس الوقت ، أي

آر إكس= 0, راي= 0, صض = 0.

لذلك ، من أجل توازن النظام المكاني للقوى المتقاربة ، من الضروري والكافي أن تكون مجاميع إسقاطات هذه القوى على كل من إحداثيات المحاور الثلاثة مساوية للصفر:

من أجل توازن نظام مسطح للقوى المتقاربة ، من الضروري والكافي أن يكون مجموع إسقاطات القوى على كل من محوري الإحداثيات مساوياً للصفر:

جمع قوتين متوازيتين في نفس الاتجاه.

الشكل 1.9

ب أ ج

R = F. 1 + ف 2

إضافة قوتين متوازيتين غير متكافئتين موجهتين في اتجاهين متعاكسين.

يتم تقليل قوتين مضادتين غير متساويتين إلى قوة ناتجة واحدة موازية لهما وتوجيههما نحو القوة الأكبر. حجم الناتج يساوي الفرق بين مقادير هذه القوى ، ونقطة تطبيقه ، C ، تقسم المسافة بين خطوط عمل القوى خارجيًا إلى أجزاء تتناسب عكسياً مع مقادير هذه القوى ، والتي يكون

زوج من القوى ولحظة القوة حول نقطة.

لحظة القوة بالنسبة إلى النقطة O ، تسمى ، مأخوذة بالإشارة المناسبة ، حاصل ضرب مقدار القوة على المسافة h من النقطة O إلى خط عمل القوة . يؤخذ هذا المنتج بعلامة الجمع إذا كانت القوة يميل إلى تدوير الجسم عكس اتجاه عقارب الساعة ، ومع علامة - ، إذا كانت القوة يميل إلى تدوير الجسم في اتجاه عقارب الساعة ، أي . طول العمودي h يسمىكتف القوة النقطة O. تأثير عمل القوة ، أي كلما كان التسارع الزاوي للجسم أكبر ، كلما زاد حجم لحظة القوة.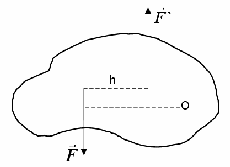

الشكل 1.11

تتم كتابتها على النحو التالي: m (F، F ") = ± F × h ، حيث يتم أخذ المنتج بعلامة زائد إذا كان زوج القوى يميل إلى تدوير الجسم عكس اتجاه عقارب الساعة وبعلامة ناقص إذا كان زوج القوى يميل لتدوير الجسم في اتجاه عقارب الساعة.

نظرية مجموع لحظات قوى الزوج.

مجموع لحظات قوى الزوج (F ، F ") فيما يتعلق بأي نقطة 0 مأخوذة في مستوى عمل الزوج لا يعتمد على اختيار هذه النقطة ويساوي لحظة الزوج.

نظرية على أزواج متكافئة. الآثار.

نظرية. زوجان تتساوى لحظاتهما مع بعضهما البعض ، أي (F، F ") ~ (P، P")

النتيجة الطبيعية 1 . يمكن نقل زوج من القوى إلى أي مكان في مستوى حركته ، وكذلك تدويره إلى أي زاوية وتغيير ذراع وحجم قوى الزوج ، مع الحفاظ على لحظة الزوج.

النتيجة 2. لا توجد نتيجة ناتجة عن زوج من القوى ولا يمكن موازنتها بقوة واحدة موجودة في مستوى الزوج.

الشكل 1.12

شرط الجمع والتوازن لنظام من الأزواج على مستوى.

1. نظرية إضافة أزواج ترقد في نفس المستوى. يمكن استبدال نظام الأزواج ، الموجود بشكل تعسفي في نفس المستوى ، بزوج واحد ، اللحظة التي تساوي مجموع لحظات هذه الأزواج.

2. نظرية حول توازن نظام الأزواج على المستوى.

من أجل أن يكون جسم جامد تمامًا في حالة راحة تحت تأثير نظام من الأزواج ، يقع بشكل تعسفي في نفس المستوى ، من الضروري والكافي أن يكون مجموع لحظات جميع الأزواج مساويًا للصفر ، أي

مركز الجاذبية

قوة الجاذبية - ناتج قوى الجذب للأرض الموزعة على كامل حجم الجسم.

مركز ثقل الجسم - هذه نقطة مرتبطة دائمًا بهذا الجسم ، والتي يمر من خلالها خط عمل قوة الجاذبية لجسم معين في أي موضع من الجسم في الفضاء.

طرق إيجاد مركز الثقل

1. طريقة التناظر:

1.1. إذا كان لجسم متجانس مستوى متماثل ، فإن مركز الجاذبية يكمن في هذا المستوى

1.2 إذا كان لجسم متجانس محور تناظر ، فإن مركز الثقل يقع على هذا المحور. يقع مركز الثقل لجسم ثورة متجانس على محور الثورة.

1.3 إذا كان لجسم متجانس محوري تناظر ، يكون مركز الجاذبية عند نقطة تقاطعهم.

2. طريقة التقسيم: ينقسم الجسم إلى أصغر عدد من الأجزاء ، وتعرف قوى الجاذبية وموضع مراكز الجاذبية.

3. طريقة الكتل السالبة: عند تحديد مركز ثقل الجسم ذي التجاويف الحرة ، يجب استخدام طريقة التقسيم ، ولكن يجب اعتبار كتلة التجاويف الحرة سالبة.

إحداثيات مركز الجاذبية شخصية مسطحة:

يمكن حساب مواضع مراكز الثقل للأشكال الهندسية البسيطة باستخدام الصيغ المعروفة. (الشكل 1.13)

ملحوظة: يقع مركز ثقل التماثل في الشكل على محور التناظر.

يقع مركز ثقل القضيب في منتصف الارتفاع.

1.2 أمثلة على حل المشكلات العملية

مثال 1: يُعلَّق وزن على قضيب وهو في حالة اتزان. حدد القوى في الشريط. (الشكل 1.2.1)

المحلول:

تتساوى القوى التي تنشأ في قضبان التثبيت من حيث الحجم مع القوى التي تدعم بها قضبان الحمل. (البديهية الخامسة)

نحدد الاتجاهات المحتملة لردود فعل السندات "القضبان الصلبة".

يتم توجيه الجهود على طول القضبان.

الشكل 1.2.1.

لنبدأ البناء بقوة معروفة برسم متجهFعلى نطاق معين.

من نهاية المتجهFرسم خطوط موازية لردود الفعلص 1 وص 2 .

الشكل 1.2.2

لإجراء حسابات أكثر دقة ، يمكنك استخدام العلاقات الهندسية ، ولا سيما نظرية الجيب: نسبة ضلع المثلث إلى جيب الزاوية المقابلة هي قيمة ثابتة

لهذه الحالة:

الشكل 1.2.3

تعليق: إذا لم يتطابق اتجاه المتجه (تفاعل الاقتران) على مخطط معين وفي مثلث القوى ، فيجب توجيه رد الفعل على المخطط في الاتجاه المعاكس.

المثال 2: حدد مقدار واتجاه النظام المسطح الناتج للقوى المتقاربة بطريقة تحليلية.

المحلول:

الشكل 1.2.4

بإضافة الإسقاطات جبريًا ، نحصل على إسقاط الناتج على محور الثور.

تشير العلامة إلى أن الناتج موجه إلى اليسار.

2. نحدد توقعات جميع القوى على محور Oy:

بإضافة الإسقاطات جبريًا ، نحصل على إسقاط الناتج على محور Oy.

تشير العلامة إلى أن الناتج يكون موجهاً نحو الأسفل.

3. حدد معامل الناتج بمقادير الإسقاطات:

4. تحديد قيمة زاوية الناتج مع محور الثور:

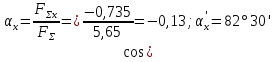
وقيمة الزاوية مع المحور y:

المثال 3: احسب مجموع لحظات القوى بالنسبة للنقطة O (الشكل 1.2.6).

OA= AB= فيD = DE = CB = 2م

الشكل 1.2.6

المحلول:

1. إن عزم القوة بالنسبة إلى نقطة ما يساوي عدديًا ناتج الوحدة وذراع القوة.

2. لحظة القوة تساوي صفرًا إذا كان خط عمل القوة يمر عبر نقطة ما.

المثال 4: حدد موضع مركز الثقل بالشكل الموضح في الشكل 1.2.7

المحلول:

نقسم الرقم إلى ثلاثة:

1-مستطيل

لكن 1 = 10 * 20 = 200 سم 2

2-مثلث

لكن 2 = 1/2 * 10 * 15 = 75 سم 2

3 لفة

لكن 3 =3,14*3 2 = 28.3 سم 2

الشكل 1 CG: x 1 = 10 سم ، ص 1 = 5 سم

الشكل 2 CG: x 2 = 20 + 1/3 * 15 = 25 سم ، ش 2 = 1/3 * 10 = 3.3 سم

الشكل 3 CG: x 3 = 10 سم ، ص 3 = 5 سم

يتم تعريفه بالمثل ل من = 4.5 سم

علم الحركة: مفاهيم أساسية.

المعلمات الحركية الأساسية

مسار - الخط الذي تحدده النقطة المادية عند التحرك في الفضاء. يمكن أن يكون المسار خطًا مستقيمًا ومنحنىًا وخطًا مسطحًا ومكانيًا.

معادلة مسار حركة الطائرة: y =F ( x)

المسافة المقطوعة. يقاس المسار على طول المسار في اتجاه السفر. تعيين -س، وحدات القياس - متر.

معادلة حركة النقطة هي معادلة تحدد موضع النقطة المتحركة كدالة للوقت.

الشكل 2.1

الشكل 2.2

في حالة الحركة المكانية ، يضاف أيضًا إحداثي ثالثض= F 3 ( ر)

هذا النوع من الحركة يسمىتنسيق .

سرعة السفر هي كمية متجهة تميز في هذه اللحظةسرعة واتجاه الحركة على طول المسار.

السرعة عبارة عن متجه موجه في أي لحظة بشكل عرضي للمسار نحو اتجاه الحركة (الشكل 2.3).

الشكل 2.3

متوسط ​​السرعة على الطريق Δسمعرف:

أين∆S- المسافة المقطوعة في الزمن Δر; Δ ر- الفاصل الزمني.

إذا كانت نقطة ما تسافر في مسارات غير متساوية في فترات زمنية متساوية ، فسيتم استدعاء الحركةمتفاوتة . في هذه الحالة ، تكون السرعة متغيرة وتعتمد على الوقتالخامس= F( ر)

يتم تعريف السرعة الحالية على أنها

تسريع النقطة - كمية متجهية تحدد معدل تغير السرعة في الحجم والاتجاه.

تتغير سرعة النقطة عند الانتقال من النقطة M1 إلى النقطة Mg في الحجم والاتجاه. متوسط ​​قيمة التسارع لهذه الفترة الزمنية

التسارع الحالي:

عادة ، للراحة ، يتم أخذ عنصرين متعامدين بشكل متبادل في الاعتبار: عادي وعرضي (الشكل 2.4)

التسارع الطبيعي أ ن ، يميز التغيير في السرعة بـ

الاتجاه ويتم تعريفه على أنه

يتم توجيه التسارع الطبيعي دائمًا بشكل عمودي على السرعة باتجاه مركز القوس.

الشكل 2.4

يتم تحديد قيمة التسريع الكاملة على النحو التالي:

تحليل الأنواع والمعلمات الحركية للحركات

حركة موحدة - هذه حركة بسرعة ثابتة:

للحركة المنتظمة المستقيمة:

للحركة المنتظمة المنحنية:

قانون الحركة الموحدة :

حركة متغيرة متساوية – هي حركة ذات تسارع مماسي ثابت:

لحركة موحدة مستقيمة

للحركة المنتظمة المنحنية:

قانون الحركة الموحدة:

الرسوم البيانية الحركية

الرسوم البيانية الحركية - هذه الرسوم البيانية للتغيرات في المسار والسرعة والتسارع حسب الوقت.

حركة موحدة (الشكل 2.5)

الشكل 2.5

حركة متساوية المتغير (الشكل 2.6)

الشكل 2.6

أبسط حركات الجسم الصلب

حركة امامية تسمى حركة الجسم الصلب ، حيث يظل أي خط مستقيم على الجسم أثناء الحركة موازيًا لموضعه الأولي (الشكل 2.7)

الشكل 2.7

في الحركة متعدية الحركة ، تتحرك جميع نقاط الجسم بنفس الطريقة: السرعات والتسارع متماثلان في كل لحظة.

فيحركة دوارة تصف جميع نقاط الجسم الدوائر حول محور ثابت مشترك.

يسمى المحور الثابت الذي تدور حوله جميع نقاط الجسممحور الدوران.

لوصف الحركة الدورانية لجسم حول محور ثابت فقطخيارات الزاوية. (الشكل 2.8)

φ هي زاوية دوران الجسم.

ω – السرعة الزاوية تحدد التغير في زاوية الدوران لكل وحدة زمنية ؛

يتم تحديد التغير في السرعة الزاوية بمرور الوقت من خلال التسارع الزاوي:

2.2. أمثلة على حل المشكلات العملية

مثال 1: يتم إعطاء معادلة حركة النقطة. أوجد سرعة النقطة في نهاية الثانية الثالثة من الحركة ومتوسط ​​السرعة للثواني الثلاث الأولى.

المحلول:

1. معادلة السرعة

2. السرعة في نهاية الثانية الثالثة (ر=3 ج)

3. متوسط ​​السرعة

المثال 2: وفقًا لقانون الحركة المحدد ، حدد نوع الحركة والسرعة الأولية والتسارع العرضي للنقطة ووقت التوقف.

المحلول:

1. نوع الحركة: متغير بالتساوي ()
2. عند مقارنة المعادلات ، من الواضح أن

- سافر المسار الأولي قبل بدء العد التنازلي 10 م ؛

- السرعة الأولية 20 م / ث

- تسارع مماسي ثابت

- التسارع سلبي ، وبالتالي ، فإن الحركة بطيئة ، ويتم توجيه التسارع في الاتجاه المعاكس لسرعة الحركة.

3. يمكنك تحديد الوقت الذي تكون فيه سرعة النقطة مساوية للصفر.

3. الديناميات: المفاهيم الأساسية والبديهيات

ديناميات - قسم من الميكانيكا النظرية يتم فيه إقامة صلة بين حركة الأجسام والقوى المؤثرة عليها.

في الديناميكيات ، يتم حل نوعين من المشاكل:

تحديد معلمات الحركة وفقًا للقوى المحددة ؛

تحديد القوى المؤثرة على الجسم وفقًا لمعايير الحركة المعطاة.

تحتنقطة مادية يشير ضمنيًا إلى جسم معين له كتلة معينة (أي يحتوي على كمية معينة من المادة) ، ولكن ليس له أبعاد خطية (حجم متناهي الصغر من الفضاء).
معزول يتم أخذ النقطة المادية في الاعتبار ، والتي لا تتأثر بالنقاط المادية الأخرى. في العالم الحقيقي ، لا توجد نقاط مادية معزولة ، وكذلك أجسام منعزلة ، وهذا المفهوم مشروط.

مع الحركة الانتقالية ، تتحرك جميع نقاط الجسم بنفس الطريقة ، لذلك يمكن اعتبار الجسم كنقطة مادية.

إذا كانت أبعاد الجسم صغيرة مقارنة بالمسار ، فيمكن اعتبارها أيضًا نقطة مادية ، بينما تتزامن النقطة مع مركز ثقل الجسم.

أثناء الحركة الدورانية للجسم ، قد لا تتحرك النقاط بنفس الطريقة ، في هذه الحالة ، يمكن تطبيق بعض أحكام الديناميكيات فقط على النقاط الفردية ، ويمكن اعتبار الكائن المادي كمجموعة من النقاط المادية.

لذلك ، يتم تقسيم الديناميكيات إلى ديناميكيات النقطة وديناميكيات نظام المواد.

بديهيات الديناميات

البديهية الأولى ( مبدأ القصور الذاتي): في تكون أي نقطة مادية معزولة في حالة راحة أو حركة موحدة ومستقيمة حتى تخرجها القوى المطبقة من هذه الحالة.

هذه الدولة تسمى الدولةالتعطيل. أزل النقطة من هذه الحالة ، أي أعطها بعض التسارع ، ربما قوة خارجية.

كل جسم (نقطة) لهالتعطيل. مقياس القصور الذاتي هو كتلة الجسم.

الجماعية مسمىكمية المادة في الجسم في الميكانيكا الكلاسيكية ، تعتبر قيمة ثابتة. وحدة الكتلة هي كيلوجرام.

البديهية الثانية (قانون نيوتن الثاني هو القانون الأساسي للديناميات)

F = أماه

أينتي - الكتلة النقطية ، كجم ؛لكن - تسارع النقطة ، م / ث 2 .

يتناسب التسارع الذي يتم نقله إلى نقطة مادية بواسطة القوة مع حجم القوة ويتزامن مع اتجاه القوة.

تعمل الجاذبية على جميع الأجسام على الأرض ، وتضفي على الجسم تسارع السقوط الحر الموجه نحو مركز الأرض:

G = ملغ

أينز- 9.81 م / ث² ، تسارع السقوط الحر.

البديهية الثالثة (قانون نيوتن الثالث): معتكون قوى التفاعل بين جسمين متساوية في الحجم وموجهة على نفس الخط المستقيم في اتجاهات مختلفة.

عند التفاعل ، تتناسب التسارع عكسياً مع الجماهير.

البديهية الرابعة (قانون استقلالية عمل القوات): toتعمل كل قوة في نظام القوات كما لو كانت تعمل بمفردها.

التسارع الذي يمنحه نظام القوى إلى النقطة يساوي المجموع الهندسي للتسارع الذي يتم نقله إلى النقطة بواسطة كل قوة على حدة (الشكل 3.1):

الشكل 3.1

مفهوم الاحتكاك. أنواع الاحتكاك.

احتكاك- المقاومة الناتجة عن حركة جسم خشن على سطح آخر. ينتج عن الاحتكاك الانزلاقي احتكاك انزلاقي ، ويؤدي الاحتكاك المتدحرج إلى احتكاك هزاز.

انزلاق الاحتكاك

الشكل 3.2.