Přednáškový kurz teoretické mechaniky. Dynamika

Jako součást jakéhokoli učebního plánu začíná studium fyziky mechanikou. Ne z teoretické, ne z aplikované a ne výpočetní, ale ze staré dobré klasické mechaniky. Tato mechanika se také nazývá newtonovská mechanika. Podle legendy se vědec procházel po zahradě, viděl padat jablko a právě tento jev ho přiměl k objevu zákona univerzální gravitace. Zákon samozřejmě existoval odjakživa a Newton mu dal pouze lidem srozumitelnou formu, ale jeho zásluha je k nezaplacení. V tomto článku nebudeme co nejpodrobněji popisovat zákony newtonovské mechaniky, ale nastíníme základy, základní poznatky, definice a vzorce, které vám vždy mohou hrát do karet.

Mechanika je obor fyziky, věda, která studuje pohyb hmotných těles a interakce mezi nimi.

Samotné slovo je řeckého původu a překládá se jako „umění stavět stroje“. Před stavbou strojů nás ale čeká ještě dlouhá cesta, vydejme se tedy po stopách našich předků a budeme studovat pohyb kamenů vržených šikmo k horizontu a jablek padajících na hlavy z výšky h.

Proč studium fyziky začíná mechanikou? Protože je naprosto přirozené, nevyjít to z termodynamické rovnováhy?!

Mechanika je jednou z nejstarších věd a historicky studium fyziky začalo právě se základy mechaniky. Lidé, umístěni v rámci času a prostoru, ve skutečnosti nemohli začít od něčeho jiného, ​​bez ohledu na to, jak moc chtěli. Pohybující se těla jsou první věcí, které věnujeme pozornost.

co je pohyb?

Mechanický pohyb je změna polohy těles v prostoru vůči sobě v čase.

Právě po této definici se zcela přirozeně dostáváme k pojmu referenční rámec. Změna polohy těles v prostoru vůči sobě navzájem. Klíčová slova tady: vůči sobě navzájem . Koneckonců, cestující v autě se pohybuje ve vztahu k osobě stojící na kraji silnice určitou rychlostí a vzhledem ke svému sousedovi leží na sedadle poblíž a pohybuje se jinou rychlostí vzhledem k cestujícímu v autě, které předběhne je.

Proto, abychom normálně změřili parametry pohybujících se objektů a nepletli se, potřebujeme referenční systém - pevně propojené referenční těleso, souřadnicový systém a hodiny. Země se například pohybuje kolem Slunce v heliocentrické vztažné soustavě. V každodenním životě provádíme téměř všechna naše měření v geocentrickém referenčním systému spojeném se Zemí. Země je referenční těleso, vůči kterému se pohybují auta, letadla, lidé, zvířata.

Mechanika jako věda má svůj vlastní úkol. Úkolem mechaniky je v každém okamžiku znát polohu tělesa v prostoru. Jinými slovy, mechanika konstruuje matematický popis pohybu a nachází souvislosti mezi fyzikálními veličinami, které jej charakterizují.

Abychom se posunuli dále, potřebujeme pojem „ hmotný bod ". Říká se, že fyzika je exaktní věda, ale fyzici vědí, kolik aproximací a předpokladů je třeba udělat, aby se shodli na této přesnosti. Nikdo nikdy neviděl hmotný bod nebo nečuchal ideální plyn, ale existují! Život s nimi je mnohem jednodušší.

Hmotný bod je těleso, jehož velikost a tvar lze v rámci tohoto problému zanedbat.

Úseky klasické mechaniky

Mechanika se skládá z několika částí

• Kinematika
• Dynamika
• Statika

Kinematika z fyzikálního hlediska studuje přesně, jak se tělo pohybuje. Jinými slovy, tato část se zabývá kvantitativními charakteristikami pohybu. Najít rychlost, dráhu - typické úlohy kinematiky

Dynamikařeší otázku, proč se pohybuje tak, jak se pohybuje. To znamená, že uvažuje síly působící na tělo.

Statika studuje rovnováhu těles při působení sil, tedy odpovídá na otázku: proč vůbec nepadá?

Meze použitelnosti klasické mechaniky

Klasická mechanika si již nečiní nárok na to, že je vědou, která vše vysvětluje (na začátku minulého století bylo všechno úplně jinak) a má jasný rozsah použitelnosti. Obecně platí zákony klasické mechaniky pro svět nám známý z hlediska velikosti (makrosvět). Přestávají fungovat v případě světa částic, kdy je klasická mechanika nahrazena kvantovou mechanikou. Rovněž klasická mechanika je nepoužitelná pro případy, kdy k pohybu těles dochází rychlostí blízkou rychlosti světla. V takových případech se projeví relativistické efekty. Zhruba řečeno, v rámci kvantové a relativistické mechaniky - klasické mechaniky se jedná o speciální případ, kdy jsou rozměry těla velké a rychlost malá.

Obecně řečeno, kvantové a relativistické efekty nikdy nezmizí, probíhají také při obvyklém pohybu makroskopických těles rychlostí mnohem nižší, než je rychlost světla. Další věcí je, že působení těchto efektů je tak malé, že nepřesahuje nejpřesnější měření. Klasická mechanika tak nikdy neztratí svůj zásadní význam.

Ve studiu fyzikálních základů mechaniky budeme pokračovat v dalších článcích. Pro lepší pochopení mechaniky můžete vždy odkazovat naši autoři, které jednotlivě vrhají světlo na temnou skvrnu nejtěžšího úkolu.

1 snímek

Průběh přednášek na teoretická mechanika Dynamika (část) Bondarenko A.N. Moskva - 2007 Elektronický výcvikový kurz byl napsán na základě přednášek autorky pro studenty studující v oborech SZhD, PGS a SDM na NIIZhT a MIIT (1974-2006). Vzdělávací materiál odpovídá kalendářní plány přes tři semestry. Chcete-li plně implementovat efekty animace během prezentace, musíte použít prohlížeč Power Point, který není nižší než ten, který je integrován do sady Microsoft Office operačního systému Windows-XP Professional. Připomínky a návrhy je možné zasílat na e-mail: [e-mail chráněný]. Moskva Státní univerzitaŽeleznice (MIIT) Katedra teoretické mechaniky Vědeckotechnické centrum dopravních technologií

2 snímek

Obsah Přednáška 1. Úvod do dynamiky. Zákony a axiomy dynamiky hmotných bodů. Základní rovnice dynamiky. Diferenciální a přirozené pohybové rovnice. Dva hlavní úkoly dynamiky. Příklady řešení přímé úlohy dynamiky Přednáška 2. Řešení inverzní úlohy dynamiky. Obecné pokyny pro řešení inverzní úlohy dynamiky. Příklady řešení inverzní úlohy dynamiky. Pohyb tělesa vrženého pod úhlem k horizontu bez zohlednění odporu vzduchu. Přednáška 3. Přímé kmity hmotného bodu. Podmínka pro vznik oscilací. Klasifikace vibrací. Volné vibrace bez zohlednění sil odporu. tlumené vibrace. Snížení oscilace. Přednáška 4. Vynucené kmitání hmotného bodu. Rezonance. Vliv odporu na pohyb při vynucených vibracích. Přednáška 5. Relativní pohyb hmotného bodu. Setrvačné síly. Konkrétní případy pohybu pro různé druhy přenosného pohybu. Vliv rotace Země na rovnováhu a pohyb těles. Přednáška 6. Dynamika mechanické soustavy. mechanický systém. Vnější a vnitřní síly. Těžiště systému. Věta o pohybu těžiště. Ochranné zákony. Příklad řešení úlohy použití věty o pohybu těžiště. Přednáška 7. Impuls síly. Množství pohybu. Věta o změně hybnosti. Ochranné zákony. Eulerova věta. Příklad řešení úlohy o použití věty o změně hybnosti. moment hybnosti. Věta o změně momentu hybnosti Přednáška 8. Zákony zachování. Základy teorie momentů setrvačnosti. Kinetický moment tuhého tělesa. Diferenciální rovnice rotace tuhého tělesa. Příklad řešení problému použití věty o změně momentu hybnosti soustavy. Základní teorie gyroskopu. Doporučená literatura 1. Yablonsky A.A. Kurz teoretické mechaniky. Část 2. M.: Vyšší škola. 1977. 368 s. 2. Meshchersky I.V. Sbírka úloh z teoretické mechaniky. M.: Věda. 1986 416 s. 3. Sbírka úkolů pro semestrální práce/ Ed. A.A. Yablonsky. M.: Vyšší škola. 1985. 366 s. 4. Bondarenko A.N. „Teoretická mechanika v příkladech a úlohách. Dynamics“ (elektronická příručka www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 snímek

Přednáška 1 Dynamika je část teoretické mechaniky, která studuje mechanický pohyb z nejobecnějšího hlediska. Pohyb je uvažován v souvislosti se silami působícími na předmět. Sekce se skládá ze tří částí: Dynamika hmotného bodu Dynamika Dynamika mechanického systému Analytická mechanika ■ Dynamika bodu - studuje pohyb hmotného bodu s přihlédnutím k silám, které tento pohyb způsobují. Hlavním objektem je hmotný bod - hmotné těleso s hmotou, jehož rozměry lze zanedbat. Základní předpoklady: - existuje absolutní prostor (má čistě geometrické vlastnosti, které nezávisí na hmotě a jejím pohybu. - existuje absolutní čas (nezávisí na hmotě a jejím pohybu). Z toho vyplývá: - existuje absolutně nepohyblivá vztažná soustava - čas nezávisí na pohybu vztažné soustavy - hmotnosti pohybujících se bodů nezávisí na pohybu vztažné soustavy Tyto předpoklady se používají v klasické mechanice vytvořené Galileem a Newtonem Má stále poměrně široký záběr, neboť mechanické systémy uvažované v aplikovaných vědách nemají tak velké hmotnosti a rychlosti pohybu, u kterých je třeba brát v úvahu jejich vliv na geometrii prostoru, času, pohybu, např. se provádí v relativistické mechanice (teorie relativity) ■ Základní zákony dynamiky - poprvé objevené Galileem a formulované Newtonem tvoří základ všech metod pro popis a analýzu pohybu mechanických systémů a jejich dynamické interakce působení pod vlivem různých sil. ■ Zákon setrvačnosti (Galileo-Newtonův zákon) - Izolovaný hmotný bod tělesa si zachovává klidový nebo rovnoměrný přímočarý pohyb, dokud jej aplikované síly nedonutí tento stav změnit. To implikuje ekvivalenci stavu klidu a pohybu setrvačností (Galileův zákon relativity). Vztažná soustava, ve vztahu ke které je splněn zákon setrvačnosti, se nazývá inerciální. Vlastnost hmotného bodu snažit se udržet rychlost svého pohybu (jeho kinematický stav) nezměněnou se nazývá setrvačnost. ■ Zákon úměrnosti síly a zrychlení (Základní rovnice dynamiky - Newtonův II zákon) - Zrychlení udělované hmotnému bodu silou je přímo úměrné síle a nepřímo úměrné hmotnosti tohoto bodu: nebo Zde m je hmotnost bodu (míra setrvačnosti), měřená v kg, číselně se rovná hmotnosti dělené gravitačním zrychlením: F je působící síla měřená v N (1 N uděluje hmotnému bodu zrychlení 1 m/s2 1 kg, 1 N \u003d 1/9. 81 kg-s). ■ Dynamika mechanického systému - studuje pohyb množiny hmotných bodů a pevných těles, spojených obecnými zákony interakce, s přihlédnutím k silám, které tento pohyb způsobují. ■ Analytická mechanika - studuje pohyb nevolných mechanických systémů pomocí obecných analytických metod. jeden

4 snímek

Přednáška 1 (pokračování - 1.2) Diferenciální rovnice pohyb hmotného bodu: - diferenciální pohybová rovnice bodu ve vektorovém tvaru. - diferenciální rovnice pohybu bodu v souřadnicovém tvaru. Tento výsledek lze získat formální projekcí vektorové diferenciální rovnice (1). Po seskupení se vektorový vztah rozloží na tři skalární rovnice: V souřadnicovém tvaru: Použijeme vztah poloměr-vektor se souřadnicemi a vektor síly s průměty: diferenciální rovnice pohybu na přirozených (pohyblivých) souřadných osách: nebo: - přirozené pohybové rovnice bodu. ■ Základní dynamická rovnice: - odpovídá vektorovému způsobu zadání pohybu bodu. ■ Zákon nezávislosti působení sil - Zrychlení hmotného bodu při působení více sil se rovná geometrickému součtu zrychlení bodu od působení každé ze sil zvlášť: nebo Platí zákon. pro jakýkoli kinematický stav těles. Síly interakce působící na různé body (těla) nejsou vyvážené. ■ Zákon rovnosti akce a reakce (Newtonův zákon III) - Každá akce odpovídá stejné a opačně zaměřené reakci: 2

5 snímek

Dva hlavní problémy dynamiky: 1. Přímý problém: Pohyb je dán (pohybové rovnice, trajektorie). Je třeba určit síly, při jejichž působení k danému pohybu dochází. 2. Inverzní úloha: Jsou dány síly, při jejichž působení k pohybu dochází. Je nutné najít parametry pohybu (pohybové rovnice, trajektorie pohybu). Obě úlohy jsou řešeny pomocí základní rovnice dynamiky a jejího průmětu na souřadnicové osy. Uvažuje-li se pohyb nevolného bodu, pak se stejně jako ve statice využívá principu uvolnění z vazeb. V důsledku reakce se vazby zahrnou do složení sil působících na hmotný bod. Řešení prvního problému je spojeno s derivačními operacemi. Řešení inverzní úlohy vyžaduje integraci odpovídajících diferenciálních rovnic, a to je mnohem obtížnější než derivování. Inverzní problém je obtížnější než přímý problém. Řešení přímé úlohy dynamiky - podívejme se na příklady: Příklad 1. Kabina o hmotnosti G výtahu je zvedána lanem se zrychlením a . Určete napětí kabelu. 1. Vyberte objekt (výtahová kabina se pohybuje vpřed a lze ji považovat za hmotný bod). 2. Spoj (lanko) vyhodíme a nahradíme reakcí R. 3. Sestavte základní dynamickou rovnici: Určete reakci lanka: Určete napnutí lanka: Při rovnoměrném pohybu kabiny ay = 0 a napnutí lanka se rovná hmotnosti: T = G. Když se lanko přetrhne T = 0 a zrychlení kabiny se rovná zrychlení volného pádu: ay = -g. 3 4. Na osu y promítneme základní rovnici dynamiky: y Příklad 2. Hmotný bod m se pohybuje po vodorovné ploše (rovina Oxy) podle rovnic: x = a coskt, y = b coskt. Určete sílu působící na bod. 1. Vyberte objekt (hmotný bod). 2. Spojení (rovinu) zahodíme a nahradíme reakcí N. 3. Do soustavy sil přidáme neznámou sílu F. 4. Sestavíme základní rovnici dynamiky: 5. Promítneme základní rovnici dynamiky na osy x,y: Určete průměty sil: Modul síly: Směrové kosiny: Velikost síly je tedy úměrná vzdálenosti bodu ke středu souřadnic a směřuje ke středu podél čáry spojující bod se středem. Trajektorie pohybu bodu je elipsa se středem v počátku: O r Přednáška 1 (pokračování - 1.3)

6 snímek

Přednáška 1 (pokračování 1.4) Příklad 3: Břemeno o hmotnosti G je zavěšeno na laně délky l a pohybuje se po kruhové dráze ve vodorovné rovině určitou rychlostí. Úhel odchylky kabelu od svislice je roven. Určete napětí lanka a rychlost zatížení. 1. Vyberte objekt (náklad). 2. Spojení (lano) zlikvidujte a nahraďte jej reakcí R. 3. Sestavte hlavní rovnici dynamiky: Ze třetí rovnice určete reakci kabelu: Určete napětí kabelu: Dosaďte hodnotu reakce lana, do druhé rovnice normálové zrychlení a určete rychlost zatížení: 4. Promítněte hlavní rovnici dynamika nápravy,n,b: Příklad 4: Automobil o hmotnosti G se pohybuje po konvexním mostě (poloměr zakřivení je R ) s rychlostí V. Určete tlak vozu na most. 1. Vybereme objekt (auto, zanedbáme rozměry a považujeme ho za bod). 2. Spojení (hrubý povrch) zahodíme a nahradíme reakcemi N a třecí silou Ffr. 3. Složíme základní rovnici dynamiky: 4. Na osu n promítneme základní rovnici dynamiky: Odtud určíme normálovou reakci: Určíme tlak auta na most: Odtud můžeme určit rychlost. odpovídající nulovému tlaku na můstku (Q = 0): 4

7 snímek

Přednáška 2 Po dosazení nalezených hodnot konstant získáme: Při působení stejného systému sil tedy může hmotný bod vykonávat celou třídu pohybů určených počátečními podmínkami. Počáteční souřadnice berou v úvahu počáteční polohu bodu. Počáteční rychlost, daná průměty, zohledňuje vliv na její pohyb po uvažovaném úseku trajektorie sil, které na bod působily před příchodem do tohoto úseku, tzn. počáteční kinematický stav. Řešení inverzní úlohy dynamiky - V obecném případě pohybu bodu jsou síly působící na bod veličinami, které jsou závislé na čase, souřadnicích a rychlosti. Pohyb bodu je popsán soustavou tří diferenciálních rovnic druhého řádu: Po integraci každé z nich bude existovat šest konstant C1, C2,…., C6: Hodnoty konstant C1, C2,… ., C6 se nalézají ze šesti počátečních podmínek při t = 0: Příklad 1 řešení inverzní úlohy: Volný hmotný bod o hmotnosti m se pohybuje působením síly F, která je konstantní co do velikosti a velikosti. . V počátečním okamžiku byla rychlost bodu v0 a shodovala se ve směru se silou. Určete pohybovou rovnici bodu. 1. Sestavíme základní rovnici dynamiky: 3. Snížíme řád derivace: 2. Zvolíme kartézský vztažný systém, směrující osu x ve směru síly a na tuto osu promítneme hlavní rovnici dynamiky: nebo x y z 4. Oddělte proměnné: 5. Vypočítejte integrály z obou částí rovnice : 6. Představme si průmět rychlosti jako časovou derivaci souřadnice: 8. Vypočítejte integrály obou částí rovnice: 7. Oddělte proměnné: 9. K určení hodnot konstant C1 a C2 použijeme počáteční podmínky t = 0, vx = v0 , x = x0: Výsledkem je rovnice rovnoměrně proměnného pohybu (podél osa x): 5

8 snímek

Obecné pokyny pro řešení přímých a inverzních úloh. Postup řešení: 1. Sestavení diferenciální pohybové rovnice: 1.1. Vyberte si souřadnicový systém - obdélníkový (pevný) s neznámou trajektorií pohybu, přirozený (pohybující se) se známou trajektorií, například kruh nebo přímka. V druhém případě lze použít jednu přímočarou souřadnici. Referenční bod by měl být kombinován s počáteční polohou bodu (v t = 0) nebo s rovnovážnou polohou bodu, pokud existuje, například když bod kolísá. 6 1.2. Nakreslete bod na pozici odpovídající libovolnému časovému okamžiku (pro t > 0) tak, aby souřadnice byly kladné (s > 0, x > 0). Předpokládáme také, že projekce rychlosti v této poloze je také pozitivní. V případě kmitů mění projekce rychlosti znaménko např. při návratu do rovnovážné polohy. Zde je třeba předpokládat, že v uvažovaném časovém okamžiku se bod vzdaluje od rovnovážné polohy. Implementace tohoto doporučení je důležitá do budoucna při práci s odporovými silami závislými na rychlosti. 1.3. Uvolněte hmotný bod z vazeb, nahraďte jejich působení reakcemi, přidejte činné síly. 1.4. Zapište základní zákon dynamiky ve vektorové podobě, promítněte na vybrané osy, vyjádřete dané nebo reaktivní síly v čase, souřadnicích nebo rychlostních proměnných, pokud na nich závisí. 2. Řešení diferenciálních rovnic: 2.1. Snižte derivaci, pokud rovnice není redukována na kanonickou (standardní) formu. například: nebo 2.2. Samostatné proměnné, například: nebo 2.4. Vypočítejte neurčité integrály na levé a pravé straně rovnice, například: 2.3. Pokud jsou v rovnici tři proměnné, pak proveďte změnu proměnných, například: a pak proměnné oddělte. Komentář. Místo počítání neurčité integrály je možné počítat určité integrály s proměnnou horní mezí. Spodní meze představují počáteční hodnoty proměnných (počáteční podmínky). Potom není třeba samostatně hledat konstantu, která je automaticky zahrnuta do řešení, například: Pomocí počátečních podmínek, například t = 0 , vx = vx0, určete integrační konstantu: 2.5. Vyjádřete rychlost například pomocí časové derivace souřadnice a opakujte kroky 2.2 -2.4 Poznámka. Pokud je rovnice redukována na kanonickou formu, která má standardní řešení, pak se použije toto hotové řešení. Konstanty integrace se stále nacházejí z počátečních podmínek. Viz např. oscilace (přednáška 4, str. 8). Přednáška 2 (pokračování 2.2)

9 snímek

Přednáška 2 (pokračování 2.3) Příklad 2 řešení inverzní úlohy: Síla závisí na čase. Zátěž o hmotnosti P se začne pohybovat po hladké vodorovné ploše působením síly F, jejíž velikost je úměrná času (F = kt). Určete vzdálenost, kterou náklad urazí za čas t. 3. Sestavte základní rovnici dynamiky: 5. Zmenšete řád derivace: 4. Promítněte základní rovnici dynamiky na osu x: nebo 7 6. Oddělte proměnné: 7. Vypočítejte integrály obou částí rovnice. rovnice: 9. Představte průmět rychlosti jako derivaci souřadnice vzhledem k času: 10. Vypočítejte integrály obou částí rovnice: 9. Oddělte proměnné: 8. Určete hodnotu konstanty C1 z počáteční podmínka t = 0, vx = v0=0: Ve výsledku získáme pohybovou rovnici (po ose x), která udává hodnotu ujeté vzdálenosti za čas t: 1. Zvolíme vztažnou soustavu (kartézskou souřadnice), aby těleso mělo kladnou souřadnici: 2. Předmět pohybu vezmeme jako hmotný bod (těleso se pohybuje vpřed), uvolníme jej ze spojení (referenční rovina) a nahradíme reakcí (normální reakce a hladký povrch) : 11. Určete hodnotu konstanty C2 z počáteční podmínky t = 0, x = x0=0: Příklad 3 řešení inverzní úlohy: Síla závisí na souřadnici. Hmotný bod o hmotnosti m je vymrštěn směrem vzhůru z povrchu Země rychlostí v0. Gravitační síla Země je nepřímo úměrná druhé mocnině vzdálenosti od bodu k těžišti (středu Země). Určete závislost rychlosti na vzdálenosti y od středu Země. 1. Vztažnou soustavu (kartézské souřadnice) volíme tak, aby těleso mělo kladnou souřadnici: 2. Sestavíme základní rovnici dynamiky: 3. Základní rovnici dynamiky promítneme na osu y: nebo Koeficient úměrnosti může zjistíme pomocí hmotnosti bodu na povrchu Země: R Proto diferenciál vypadá takto: nebo 4. Snižte řád derivace: 5. Změňte proměnnou: 6. Oddělte proměnné: 7. Vypočítejte integrály obou stran rovnice: 8. Dosaďte limity: Výsledkem je vyjádření rychlosti v závislosti na souřadnici y: Maximální výškový let lze zjistit přirovnáním rychlosti k nule: Maximální výška letu když se jmenovatel otočí na nulu: Odtud při nastavení poloměru Země a zrychlení volného pádu se získá II kosmická rychlost:

10 snímek

Přednáška 2 (pokračování 2.4) Příklad 2 řešení inverzní úlohy: Síla závisí na rychlosti. Loď o hmotnosti m měla rychlost v0. Odpor vody vůči pohybu lodi je úměrný rychlosti. Určete dobu, za kterou rychlost lodi po vypnutí motoru klesne na polovinu, a také vzdálenost, kterou loď urazí do úplného zastavení. 8 1. Vztažnou soustavu (kartézské souřadnice) zvolíme tak, aby těleso mělo kladnou souřadnici: 2. Předmět pohybu vezmeme jako hmotný bod (loď se pohybuje vpřed), zbavíme ho vazeb (voda) a nahradíme s reakcí (vztlaková síla - Archimédova síla), a také síla odporu vůči pohybu. 3. Přidejte aktivní sílu (gravitaci). 4. Sestavíme hlavní rovnici dynamiky: 5. Hlavní rovnici dynamiky promítneme na osu x: nebo 6. Snížíme řád derivace: 7. Oddělíme proměnné: 8. Z obou vypočítáme integrály. části rovnice: 9. Dosadíme meze: Získáme výraz, který dává do vztahu rychlost a čas t, ze kterého lze určit čas pohybu: Čas pohybu, během kterého rychlost klesne na polovinu: Je zajímavé je, že když se rychlost blíží nule, doba pohybu má tendenci k nekonečnu, tzn. konečná rychlost nemůže být nulová. Proč ne "perpetum mobile"? V tomto případě je však ujetá vzdálenost do zastávky konečná hodnota. Abychom určili ujetou vzdálenost, přejdeme k výrazu získanému po snížení řádu derivace a provedeme změnu proměnné: Po integraci a dosazení limit získáme: Vzdálenost ujetá na doraz: ■ Pohyb bodu vrženého na úhel k horizontu v rovnoměrném gravitačním poli bez zohlednění odporu vzduchu Vyloučením času z pohybových rovnic získáme rovnici trajektorie: Doba letu je určena přirovnáním souřadnice y k nule: Dosah letu je určen dosazením doba letu:

11 snímek

Přednáška 3 Přímé kmity hmotného bodu - K kmitavý pohyb hmotného bodu dochází za podmínky, že působí vratná síla, která má tendenci vrátit bod do rovnovážné polohy při jakékoli odchylce od této polohy. 9 Existuje vratná síla, rovnovážná poloha je stabilní Žádná vratná síla, rovnovážná poloha je nestabilní Žádná vratná síla, rovnovážná poloha je indiferentní Směřuje vždy do rovnovážné polohy, hodnota je přímo úměrná lineárnímu prodloužení (zkrácení) pružiny, rovna výchylce tělesa z rovnovážné polohy: c je koeficient tuhosti pružiny, číselně stejnou silou, při jehož působení pružina změní svou délku o jednu, se v soustavě SI měří v N/m. x y O Druhy vibrací hmotného bodu: 1. Volné vibrace (bez zohlednění odporu média). 2. Volné kmity zohledňující odpor média (tlumené kmity). 3. Nucené vibrace. 4. Nucené kmity s přihlédnutím k odporu média. ■ Volné kmity - vznikají působením pouze vratné síly. Zapišme si základní zákon dynamiky: Zvolme souřadný systém se středem v rovnovážné poloze (bod O) a rovnici promítneme na osu x: Uveďme výslednou rovnici do standardního (kanonického) tvaru: Tato rovnice je homogenní. lineární diferenciální rovnice druhého řádu, jejíž tvar řešení je určen kořeny charakteristické rovnice získané pomocí univerzální substituce: Kořeny charakteristické rovnice jsou myšlené a rovny: Obecné řešení diferenciální rovnice má tvar: Bodová rychlost: Počáteční podmínky: Definujte konstanty: Takže rovnice volné vibrace má tvar: Rovnici lze znázornit jednočlenným výrazem: kde a je amplituda, je počáteční fáze. Nové konstanty a a - souvisí s konstantami C1 a C2 vztahy: Definujme a a: Důvodem vzniku volných kmitů je počáteční posunutí x0 a/nebo počáteční rychlost v0.

12 snímek

10 Přednáška 3 (pokračování 3.2) Tlumené kmity hmotného bodu - K kmitavý pohyb hmotného bodu dochází za přítomnosti vratné síly a síly odporu vůči pohybu. Závislost síly odporu vůči pohybu na posuvu nebo rychlosti je dána fyzikální povahou média nebo spojení, které pohybu brání. Nejjednodušší závislost je lineární závislost na rychlosti (viskózní odpor): - viskozitní koeficient x y O Základní rovnice dynamiky: Průmět rovnice dynamiky na osu: standardní pohled: kde Charakteristická rovnice má kořeny: Obecné řešení této diferenciální rovnice má různý tvar v závislosti na hodnotách kořenů: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - případ vysokého viskózního odporu: - skutečné kořeny, různé. nebo - tyto funkce jsou aperiodické: 3. n = k: - kořeny jsou reálné, násobné. tyto funkce jsou také aperiodické:

13 snímek

Přednáška 3 (pokračování 3.3) Klasifikace řešení volných kmitů. Pružinové spoje. ekvivalentní tvrdost. y y 11 Dif. Znak rovnice. Kořeny rovnice char. rovnice Řešení diferenciální rovnice Graf nk n=k

14 snímek

Přednáška 4 Vynucené kmitání hmotného bodu - Spolu s vratnou silou působí periodicky se měnící síla, nazývaná rušivá síla. Rušivá síla může mít různou povahu. Například v konkrétním případě setrvačný účinek nevyvážené hmoty m1 rotujícího rotoru způsobuje harmonicky se měnící průměty sil: Hlavní rovnice dynamiky: Průmět rovnice dynamiky na osu: Uveďme rovnici do normy tvar: 12 Řešení této nehomogenní diferenciální rovnice se skládá ze dvou částí x = x1 + x2: x1 je obecné řešení příslušné homogenní rovnice a x2 je partikulární řešení nehomogenní rovnice: Partikulární řešení vybereme ve tvaru pravá strana: Výsledná rovnost musí být splněna pro libovolné t . Potom: nebo Tedy za současného působení vratných a rušivých sil hmotný bod koná složitý kmitavý pohyb, který je výsledkem sčítání (superpozice) volných (x1) a vynucených (x2) kmitů. Pokud p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (vynucené kmity vysoké frekvence), pak je fáze kmitů opačná než fáze rušivé síly:

15 snímek

Přednáška 4 (pokračování 4.2) 13 Dynamický koeficient - poměr amplitudy vynucených kmitů ke statické výchylce bodu působením konstantní síly H = konst: Amplituda vynucených kmitů: Statickou odchylku lze zjistit z rovnice rovnováhy: Zde: Odtud: Tedy na str< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (vysoká frekvence vynucených kmitů) dynamický koeficient: Rezonance - nastává, když se frekvence vynucených kmitů shoduje s frekvencí vlastních kmitů (p = k). Nejčastěji k tomu dochází při spouštění a zastavování rotace špatně vyvážených rotorů uložených na elastických závěsech. Diferenciální rovnice kmitů se stejnými frekvencemi: Konkrétní řešení ve tvaru pravé strany nelze vzít, protože dostaneme lineárně závislé řešení (viz obecné řešení). Obecné řešení: Dosaďte v diferenciální rovnici: Vezměme konkrétní řešení ve tvaru a vypočítejme derivace: Získáme tedy řešení: nebo Vynucené kmity při rezonanci mají amplitudu, která se úměrně času neomezeně zvětšuje. Vliv odporu na pohyb při vynucených vibracích. Diferenciální rovnice za přítomnosti viskózního odporu má tvar: Obecné řešení se vybere z tabulky (Přednáška 3, str. 11) v závislosti na poměru n a k (viz). Vezmeme konkrétní řešení ve tvaru a vypočítáme derivace: Dosadíme do diferenciální rovnice: Vyrovnáním koeficientů pro shodné goniometrické funkce získáme soustavu rovnic: Umocněním obou rovnic na mocninu a jejich sečtením získáme amplitudu vynucené kmity: Vydělením druhé rovnice první získáme fázový posun vynucených kmitů: Pohybová rovnice pro vynucené kmitání se zohledněním odporu proti pohybu, např. pro n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 snímek

Přednáška 5 Relativní pohyb hmotného bodu - Předpokládejme, že pohyblivý (neinerciální) souřadný systém Oxyz se pohybuje podle nějakého zákona vůči pevnému (inerciálnímu) souřadnému systému O1x1y1z1. Pohyb hmotného bodu M (x, y, z) vzhledem k pohyblivé soustavě Oxyz je relativní, vzhledem k nehybné soustavě O1x1y1z1 absolutní. Pohyb mobilního systému Oxyz vzhledem k pevnému systému O1x1y1z1 je přenosný pohyb. 14 z x1 y1 z1 O1 x y M x y z O Základní rovnice dynamiky: Absolutní zrychlení bodu: Do hlavní rovnice dynamiky dosadíme absolutní zrychlení bodu: Přeneseme členy s translačním a Coriolisovým zrychlením na pravou stranu: přenesené členy mají rozměr sil a jsou uvažovány jako odpovídající setrvačné síly, rovné: Pak lze relativní pohyb bodu považovat za absolutní, pokud k působícím silám přičteme translační a Coriolisovy síly setrvačnosti: V průmětech do os pohyblivého souřadnicového systému máme: rotace je rovnoměrná, pak εe = 0: 2. Translační křivočarý pohyb: Je-li pohyb přímočarý, pak = : Pokud je pohyb přímočarý a rovnoměrný, pak je pohybující se soustava setrvačná a relativní pohyb lze považovat za absolutní: Žádné mechanické jevy nemohou detekovat přímočarou uniformu pohyb (princip relativity klasické mechaniky). Vliv rotace Země na rovnováhu těles - Předpokládejme, že těleso je na zemském povrchu v rovnováze na libovolné zeměpisné šířce φ (rovnoběžky). Země se otáčí kolem své osy ze západu na východ úhlovou rychlostí: Poloměr Země je asi 6370 km. SR je celková reakce nehladkého povrchu. G - síla přitažlivosti Země ke středu. Ф - odstředivá síla setrvačnosti. Podmínka relativní rovnováhy: Výslednicí sil přitažlivosti a setrvačnosti je tíhová síla (váha): Velikost tíhové síly (váhy) na povrch Země je P = mg. Odstředivá síla setrvačnosti je malým zlomkem gravitační síly: Odchylka gravitační síly od směru přitažlivé síly je také malá: Vliv rotace Země na rovnováhu těles je tedy extrémně malý. a v praktických výpočtech se nebere v úvahu. Maximální hodnota setrvačné síly (při φ = 0 - na rovníku) je pouze 0,00343 hodnoty gravitace

17 snímek

Přednáška 5 (pokračování 5.2) 15 Vliv rotace Země na pohyb těles v gravitačním poli Země - Předpokládejme, že těleso padá na Zemi z určité výšky H nad povrchem Země v zeměpisné šířce φ . Zvolme pohyblivou vztažnou soustavu, pevně spojenou se Zemí, směřující osy x, y tečně k rovnoběžce a k poledníku: Rovnice relativního pohybu: Zde je maličkost odstředivé síly setrvačnosti ve srovnání s gravitační silou. vzít v úvahu. Gravitační síla je tedy ztotožněna s gravitační silou. Navíc předpokládáme, že gravitace je nasměrována kolmo k zemskému povrchu z důvodu malosti jejího vychýlení, jak bylo diskutováno výše. Coriolisovo zrychlení se rovná a směřuje rovnoběžně s osou y na západ. Coriolisova setrvačná síla směřuje opačným směrem. Rovnici relativního pohybu promítneme na osu: Řešení první rovnice dává: Počáteční podmínky: Řešení třetí rovnice dává: Počáteční podmínky: Třetí rovnice má tvar: Počáteční podmínky: Její řešení dává: Výsledné řešení ukazuje, že se těleso při pádu odchýlí na východ. Vypočítejme si hodnotu této odchylky např. při pádu z výšky 100 m. Dobu pádu zjistíme z řešení druhé rovnice: Vliv rotace Země na pohyb těles je tedy extrémně malý. pro praktické výšky a rychlosti a není zohledněn v technických výpočtech. Řešení druhé rovnice také implikuje existenci rychlosti podél osy y, která by měla také způsobit a způsobit odpovídající zrychlení a Coriolisovu setrvačnou sílu. Vliv této rychlosti a s ní spojené setrvačné síly na změnu pohybu bude ještě menší než uvažovaná Coriolisova setrvačná síla spojená s vertikální rychlostí.

18 snímek

Přednáška 6. Dynamika mechanické soustavy. Systém hmotných bodů nebo mechanický systém - soubor hmotných bodů nebo těch hmotných bodů spojených obecnými zákony interakce (poloha nebo pohyb každého z bodů nebo tělesa závisí na poloze a pohybu všech ostatních) systém volných bodů - jehož pohyb není omezen žádnými spoji (např. planetární systém , ve kterém jsou planety považovány za hmotné body). Systém nesvobodných bodů nebo nesvobodný mechanický systém - pohyb hmotných bodů nebo těles je omezen omezeními kladenými na systém (například mechanismus, stroj atd.). 16 Síly působící na soustavu. Kromě dříve existující klasifikace sil (činné a reaktivní síly) se zavádí nová klasifikace sil: 1. Vnější síly (e) - působící na body a tělesa soustavy z bodů nebo těles, která nejsou její součástí. Systém. 2. Vnitřní síly (i) - síly interakce mezi hmotnými body nebo tělesy zahrnutými v daném systému. Stejnou silou může být vnější i vnitřní síla. Vše závisí na tom, který mechanický systém je uvažován. Například: V systému Slunce, Země a Měsíce jsou všechny gravitační síly mezi nimi vnitřní. Při uvažování soustavy Země a Měsíce jsou gravitační síly působící ze strany Slunce vnější: C Z L Na základě zákona akce a reakce každá vnitřní síla Fk odpovídá jiné vnitřní síle Fk', stejné v absolutní hodnotě a opačné v směr. Z toho vyplývají dvě pozoruhodné vlastnosti vnitřních sil: Hlavní vektor všech vnitřních sil soustavy je roven nule: Hlavní moment všech vnitřních sil soustavy vůči libovolnému středu je roven nule: Nebo v průmětech na souřadnici Obr. osy: Pozn. Ačkoli jsou tyto rovnice podobné rovnicím rovnováhy, nejsou, protože vnitřní síly působí na různé body nebo tělesa systému a mohou způsobit, že se tyto body (těla) vzájemně pohybují. Z těchto rovnic vyplývá, že vnitřní síly neovlivňují pohyb systému uvažovaného jako celku. Těžiště soustavy hmotných bodů. Pro popis pohybu soustavy jako celku se zavádí geometrický bod zvaný těžiště, jehož poloměrový vektor je určen výrazem, kde M je hmotnost celého systému: Nebo v průmětech na souřadnici osy: Vzorce pro těžiště jsou podobné jako pro těžiště. Pojem těžiště je však obecnější, protože nesouvisí s gravitačními silami nebo gravitačními silami.

19 snímek

Přednáška 6 (pokračování 6.2) 17 Věta o pohybu těžiště soustavy - Uvažujme soustavu n hmotných bodů. Síly působící na každý bod rozdělíme na vnější a vnitřní a nahradíme je odpovídajícími výslednicemi Fke a Fki. Zapišme si pro každý bod základní rovnici dynamiky: nebo Sečtěme tyto rovnice přes všechny body: Na levé straně rovnice zavedeme hmotnosti pod znaménko derivace a součet derivací nahradíme derivací. součtu: Z definice těžiště: Do výsledné rovnice dosadíme: dostaneme nebo: Součin hmotnosti soustavy a zrychlení jejího těžiště je roven hlavnímu vektoru vnějších sil. V průmětech na souřadnicové osy: Těžiště soustavy se pohybuje jako hmotný bod o hmotnosti rovnající se hmotnosti celé soustavy, na kterou působí všechny vnější síly působící na soustavu. Důsledky z věty o pohybu těžiště soustavy (zákony zachování): 1. Je-li v časovém intervalu hlavní vektor vnějších sil soustavy nulový, Re = 0, pak rychlost středu hmotnosti je konstantní, vC = konst (těžiště se pohybuje rovnoměrně přímočaře - zákon zachování pohybu těžiště). 2. Je-li v časovém intervalu průmět hlavního vektoru vnějších sil soustavy na osu x roven nule, Rxe = 0, pak je rychlost těžiště podél osy x konstantní, vCx = const (těžiště se pohybuje rovnoměrně podél osy). Podobná tvrzení platí pro osy yaz. Příklad: Dva lidé o hmotnosti m1 a m2 jsou na lodi o hmotnosti m3. V počáteční chvíli byla loď s lidmi v klidu. Určete výtlak člunu, pokud se osoba o hmotnosti m2 přesunula na příď člunu ve vzdálenosti a. 3. Pokud je v časovém intervalu hlavní vektor vnějších sil soustavy roven nule, Re = 0, a v počátečním okamžiku je rychlost těžiště nulová, vC = 0, pak je poloměr vektoru těžiště zůstává konstantní, rC = konst (těžiště je v klidu je zákon zachování polohy těžiště). 4. Je-li v časovém intervalu průmět hlavního vektoru vnějších sil soustavy na osu x roven nule, Rxe = 0 a v počátečním okamžiku je rychlost těžiště podél této osy nulová. , vCx = 0, pak souřadnice těžiště podél osy x zůstane konstantní, xC = const (těžiště se po této ose nepohybuje). Podobná tvrzení platí pro osy yaz. 1. Předmět pohybu (loď s lidmi): 2. Zahodíme souvislosti (voda): 3. Spojení nahradíme reakcí: 4. Sečtěte aktivní síly: 5. Zapište větu o těžišti: Promítněte na osu x: O Určete, jak daleko se potřebujete přesunout k osobě o hmotnosti m1, aby loď zůstala na místě: Loď se posune o vzdálenost l opačným směrem.

20 snímek

Přednáška 7 Impuls síly je mírou mechanické interakce, která charakterizuje přenos mechanického pohybu ze sil působících na bod za daný časový úsek: 18 V průmětech na souřadnicové osy: V případě konstantní síly: V průmětech na souřadnicové osy: k bodu sil ve stejném časovém intervalu: Násobit dt: Integrovat za daný časový interval: Velikost pohybu bodu je mírou mechanického pohybu, určenou vektorem rovným součinu hmotnost bodu a jeho vektor rychlosti: Věta o změně velikosti pohybu soustavy – Uvažujme soustavu n hmotných bodů. Síly působící na každý bod rozdělíme na vnější a vnitřní a nahradíme je odpovídajícími výslednicemi Fke a Fki. Napišme pro každý bod základní rovnici dynamiky: nebo Veličina pohybu soustavy hmotných bodů - geometrický součet veličin pohybu hmotných bodů: Podle definice těžiště: Vektor hybnosti soustavy Obr. se rovná součinu hmotnosti celé soustavy a vektoru rychlosti těžiště soustavy. Potom: V průmětech na souřadnicové osy: Časová derivace vektoru hybnosti soustavy je rovna hlavnímu vektoru vnějších sil soustavy. Sečteme tyto rovnice přes všechny body: Na levé straně rovnice zavedeme hmotnosti pod znaménko derivace a nahradíme součet derivací derivací součtu: Z definice hybnosti soustavy: V průmětech na souřadnicové osy:

21 snímek

Eulerova věta - Aplikace věty o změně hybnosti systému na pohyb spojitého prostředí (vody). 1. Jako objekt pohybu zvolíme objem vody nacházející se v křivočarém kanálu turbíny: 2. Spoje zahodíme a jejich působení nahradíme reakcemi (Rpov - výslednice povrchových sil) 3. Přidáme aktivní síly (Rb - výslednice tělesných sil): 4. Zapište větu o změně hybnosti soustavy: Velikost pohybu vody v časech t0 a t1 budeme reprezentovat součty: Změna hybnosti vody v časovém intervalu : Změna hybnosti vody za nekonečně malý časový interval dt: , kde F1 F2 Vezmeme-li součin hustoty, plochy průřezu a rychlosti za sekundovou hmotnost, dostaneme: Dosazením diferenciálu hybnosti soustavy do věty o změně , získáme: Důsledky z věty o změně hybnosti soustavy (zákony zachování): 1. Je-li v časovém intervalu hlavní vektor vnějších sil soustavy roven nule, Re = 0, pak veličina vektorový pohyb je konstantní, Q = konst je zákon zachování hybnosti soustavy). 2. Je-li v časovém intervalu průmět hlavního vektoru vnějších sil soustavy na osu x roven nule, Rxe = 0, pak je průmět hybnosti soustavy na ose x konstantní, Qx = konst. Podobná tvrzení platí pro osy yaz. Přednáška 7 (pokračování 7.2) Příklad: Granát o hmotnosti M letící rychlostí v se rozbil na dvě části. Rychlost jednoho z úlomků o hmotnosti m1 vzrostla ve směru pohybu na hodnotu v1. Určete rychlost druhého fragmentu. 1. Předmět pohybu (granát): 2. Předmět je volný systém, neexistují žádné souvislosti a jejich reakce. 3. Sečtěte činné síly: 4. Zapište větu o změně hybnosti: Promítněte na osu: β Rozdělte proměnné a integrujte: Správný integrál je téměř nulový, protože doba výbuchu t

22 snímek

Přednáška 7 (pokračování 7.3) 20 Moment hybnosti bodu nebo kinetický moment pohybu vzhledem k určitému středu je mírou mechanického pohybu, určenou vektorem rovným vektorovému součinu vektoru poloměru hmotného bodu a vektor jeho hybnosti: Kinetický moment soustavy hmotných bodů vzhledem k určitému středu je geometrický součet momentů počtu pohybů všech hmotných bodů vzhledem ke stejnému středu: V průmětech na osu: V průmětech na Obr. osa: Věta o změně momentu hybnosti soustavy - Uvažujme soustavu n hmotných bodů. Síly působící na každý bod rozdělíme na vnější a vnitřní a nahradíme je odpovídajícími výslednicemi Fke a Fki. Zapišme si pro každý bod základní rovnici dynamiky: nebo Sečtěme tyto rovnice pro všechny body: Nahraďme součet derivací derivací součtu: Výraz v závorce je moment hybnosti soustavy. Odtud: Každou z rovností vektorově vynásobíme poloměrovým vektorem vlevo: Podívejme se, zda je možné vzít znaménko derivace mimo vektorový součin: Tak jsme dostali: střed. V průmětech na souřadnicové osy: Derivace momentu hybnosti systému vůči nějaké ose v čase je rovna hlavnímu momentu vnějších sil systému vůči stejné ose.

23 snímek

Přednáška 8 21 ■ Důsledky z věty o změně momentu hybnosti soustavy (zákony zachování): 1. Je-li v časovém intervalu vektor hlavního momentu vnějších sil soustavy vůči určitému středu roven na nulu, MOe = 0, pak je vektor momentu hybnosti soustavy vůči stejnému středu konstantní, KO = const je zákon zachování hybnosti soustavy). 2. Je-li v časovém intervalu hlavní moment vnějších sil soustavy vůči ose x roven nule, Mxe = 0, pak je moment hybnosti soustavy vůči ose x konstantní, Kx = konst. Podobná tvrzení platí pro osy yaz. 2. Moment setrvačnosti tuhého tělesa kolem osy: Moment setrvačnosti hmotného bodu kolem osy je roven součinu hmotnosti bodu a druhé mocniny vzdálenosti bodu k ose. Moment setrvačnosti tuhého tělesa kolem osy je roven součtu součinů hmotnosti každého bodu a druhé mocniny vzdálenosti tohoto bodu od osy. ■ Prvky teorie momentů setrvačnosti - Při rotačním pohybu tuhého tělesa je mírou setrvačnosti (odpor vůči změně pohybu) moment setrvačnosti kolem osy rotace. Zvažte základní pojmy definice a metody výpočtu momentů setrvačnosti. 1. Moment setrvačnosti hmotného bodu kolem osy: Při přechodu z diskrétní malé hmotnosti do nekonečně malé hmotnosti bodu je limita takového součtu určena integrálem: osovým momentem setrvačnosti tuhého tělesa. . Kromě osového momentu setrvačnosti tuhého tělesa existují další druhy momentů setrvačnosti: odstředivý moment setrvačnosti tuhého tělesa. polární moment setrvačnosti tuhého tělesa. 3. Věta o momentech setrvačnosti tuhého tělesa o rovnoběžných osách - vzorec pro přechod na rovnoběžné osy: Moment setrvačnosti k referenční ose Statické momenty setrvačnosti k referenčním osám Hmotnost tělesa Vzdálenost mezi osami z1 a z2 Tedy : moments are zero:

24 snímek

Přednáška 8 (pokračování 8.2) 22 Moment setrvačnosti rovnoměrné tyče konstantního průřezu kolem osy: x z L Vyberte elementární objem dV = Adx ve vzdálenosti x: x dx Elementární hmotnost: Pro výpočet momentu setrvačnosti kolem centrální osy (průchod těžištěm), stačí změnit umístění osy a nastavit integrační meze (-L/2, L/2). Zde demonstrujeme vzorec pro přechod k rovnoběžným osám: zС 5. Moment setrvačnosti homogenního pevného válce kolem osy symetrie: H dr r Vyčleňme elementární objem dV = 2πrdrH (tenký válec o poloměru r) : Elementární hmotnost: Zde použijeme objemový vzorec válce V=πR2H. Pro výpočet momentu setrvačnosti dutého (tlustého) válce stačí nastavit integrační meze od R1 do R2 (R2> R1): 6. Moment setrvačnosti tenkého válce kolem osy symetrie (t

25 snímek

Přednáška 8 (pokračování 8.3) 23 ■ Diferenciální rovnice rotace tuhého tělesa kolem osy: Napíšeme větu o změně momentu hybnosti tuhého tělesa rotujícího kolem pevné osy: Hybnost rotujícího tuhého tělesa je: Moment of external forces about the axis of rotation is equal to the torque (reactions and force do not create gravity moments): We substitute the kinetic moment and torque into the theorem Example: Two people of the same weight G1 = G2 hang on a rope thrown přes pevný blok o hmotnosti G3 = G1/4. V určitém okamžiku jeden z nich začal šplhat po laně relativní rychlostí u. Určete rychlost zvedání každé osoby. 1. Vyberte objekt pohybu (blok s lidmi): 2. Vyřaďte spojení (nosné zařízení bloku): 3. Nahraďte spojení s reakcemi (ložisko): 4. Přidejte aktivní síly (gravitaci): 5. Zapište věta o změně kinetického momentu soustavy vzhledem k ose rotace bloku: R Protože moment vnějších sil je roven nule, kinetický moment musí zůstat konstantní: V počátečním okamžiku času t = 0 byl rovnovážný a Kz0 = 0. Po začátku pohybu jedné osoby vůči lanu se celý systém začal pohybovat, ale kinetický moment systému musí zůstat roven nule: Kz = 0. Moment hybnosti lana soustava je součet momentů hybnosti jak lidí, tak kvádru: Zde v2 je rychlost druhé osoby, rovna rychlosti kabelu, Příklad: Určete periodu malých volných kmitů homogenní tyče o hmotnosti M a Obr. délka l, zavěšený jedním koncem k pevné ose otáčení. Nebo: V případě malých kmitů sinφ φ: Perioda kmitání: Moment setrvačnosti tyče:

26 snímek

Přednáška 8 (pokračování 8.4 - doplňkový materiál) 24 ■ Elementární teorie gyroskopu: Gyroskop je tuhé těleso rotující kolem osy symetrie materiálu, jehož jeden z bodů je pevný. Volný gyroskop je upevněn tak, že jeho těžiště zůstává nehybné a osa rotace prochází těžištěm a může zaujímat libovolnou polohu v prostoru, tzn. osa rotace mění svou polohu jako osa rotace vlastního těla při kulovém pohybu. Hlavním předpokladem přibližné (elementární) teorie gyroskopu je, že vektor hybnosti (kinetický moment) rotoru je považován za směrovaný podél vlastní osy otáčení. Přestože se tedy v obecném případě rotor účastní tří otáček, bere se v úvahu pouze úhlová rychlost jeho vlastního otáčení ω = dφ/dt. Základem toho je, že v moderní technologie rotor gyroskopu se otáčí úhlovou rychlostí řádově 5000-8000 rad/s (asi 50000-80000 ot./min), zatímco další dvě úhlové rychlosti spojené s precesí a nutací vlastní rotační osy jsou desetitisícinásobné menší než tato rychlost. Hlavní vlastností volného gyroskopu je, že osa rotoru zachovává stejný směr v prostoru vzhledem k inerciální (hvězdné) vztažné soustavě (demonstrováno Foucaultovým kyvadlem, které udržuje rovinu výkyvu nezměněnou vzhledem ke hvězdám, 1852). Vyplývá to ze zákona zachování kinetického momentu vzhledem k těžišti rotoru za předpokladu, že se zanedbá tření v ložiskách os zavěšení rotoru, vnějšího a vnitřního rámu: Působení síly na osu vol. gyroskop. V případě síly působící na osu rotoru není moment vnějších sil vůči těžišti roven nule: ω ω С síla, a směrem k vektoru momentu této síly, tzn. se nebude otáčet kolem osy x (vnitřní zavěšení), ale kolem osy y (vnější zavěšení). Po ukončení působení síly zůstane osa rotoru ve stejné poloze, odpovídající poslední době působení síly, protože od tohoto okamžiku se moment vnějších sil opět rovná nule. V případě krátkodobého silového působení (nárazu) osa gyroskopu prakticky nemění svoji polohu. Rychlé otáčení rotoru tedy dává gyroskopu schopnost čelit náhodným vlivům, které se snaží změnit polohu osy otáčení rotoru, a při konstantním působení síly udržuje polohu roviny kolmé k operační síla, který obsahuje osu rotoru. Tyto vlastnosti se využívají při provozu inerciálních navigačních systémů.

Pohled: tento článek byl přečten 32852 krát

Pdf Vyberte jazyk... Ruština Ukrajinština Angličtina

Krátká recenze

Úplný materiál je stažen výše po výběru jazyka

• Statika
  • Základní pojmy statiky
  • Typy sil
  • Axiomy statiky
  • Spojení a jejich reakce
  • Systém konvergujících sil
    • Metody stanovení výsledné soustavy konvergujících sil
    • Podmínky rovnováhy pro soustavu konvergujících sil
  • Moment síly kolem středu jako vektor
    • Algebraická hodnota momentu síly
    • Vlastnosti momentu síly kolem středu (bodu)
  • Teorie dvojic sil
    • Sčítání dvou rovnoběžných sil ve stejném směru
    • Sčítání dvou rovnoběžných sil směřujících v opačných směrech
    • Výkonové páry
    • Věty o páru sil
    • Podmínky pro rovnováhu soustavy dvojic sil
  • Rameno páky
  • Libovolný rovinný systém sil
    • Případy redukce ploché soustavy sil na jednodušší formu
    • Podmínky analytické rovnováhy
  • Střed paralelních sil. Centrum gravitace
    • Střed paralelních sil
    • Těžiště tuhého tělesa a jeho souřadnice
    • Těžiště objemu, roviny a přímky
    • Metody určování polohy těžiště
• Základy silových závodů
  • Problémy a metody odolnosti materiálů
  • Klasifikace zatížení
  • Klasifikace konstrukčních prvků
  • Deformace tyče
  • Hlavní hypotézy a principy
  • Vnitřní síly. Sekční metoda
  • Napětí
  • Napětí a komprese
  • Mechanické vlastnosti materiálu
  • Přípustná napětí
  • Tvrdost materiálu
  • Grafy podélných sil a napětí
  • Posun
  • Geometrické charakteristiky řezů
  • Kroucení
  • ohyb
    • Diferenciální závislosti v ohybu
    • Pevnost v ohybu
    • normální stresy. Výpočet pevnosti
    • Smyková napětí v ohybu
    • Tuhost v ohybu
  • Základy obecné teorie napjatosti
  • Pevnostní teorie
  • Ohýbání s kroucením
• Kinematika
  • Bodová kinematika
    • Bodová trajektorie
    • Metody pro specifikaci pohybu bodu
    • Bodová rychlost
    • bodové zrychlení
  • Kinematika tuhého těla
    • Translační pohyb tuhého tělesa
    • Rotační pohyb tuhého tělesa
    • Kinematika převodových mechanismů
    • Rovinně paralelní pohyb tuhého tělesa
  • Složitý pohyb bodu
• Dynamika
  • Základní zákony dynamiky
  • Dynamika bodů
    • Diferenciální rovnice volného hmotného bodu
    • Dva problémy dynamiky bodu
  • Dynamika tuhého těla
    • Klasifikace sil působících na mechanickou soustavu
    • Diferenciální pohybové rovnice mechanické soustavy
  • Obecné teorémy dynamiky
    • Věta o pohybu těžiště mechanické soustavy
    • Věta o změně hybnosti
    • Věta o změně momentu hybnosti
    • Věta o změně kinetické energie
• Síly působící ve strojích
  • Síly v záběru čelního ozubeného kola
  • Tření v mechanismech a strojích
    • Kluzné tření
    • valivé tření
  • Účinnost
• Části strojů
  • Mechanické převody
    • Druhy mechanických převodů
    • Základní a odvozené parametry mechanických převodů
    • ozubená kola
    • Ozubená kola s pružnými články
  • Hřídele
    • Účel a klasifikace
    • Návrhový výpočet
    • Kontrolní výpočet hřídelí
  • Ložiska
    • Kluzná ložiska
    • Valivá ložiska
  • Spojování částí stroje
    • Typy rozebíratelných a trvalých spojů
    • Klíčová spojení
• Standardizace norem, zaměnitelnost
  • Tolerance a přistání
  • Jednotný systém tolerancí a přistání (ESDP)
  • Odchylka tvaru a polohy

Formát: pdf

Velikost: 4 MB

ruský jazyk

Příklad výpočtu čelního ozubeného kola
Příklad výpočtu čelního ozubeného kola. Byla provedena volba materiálu, výpočet dovolených napětí, výpočet dotykové a ohybové pevnosti.

Příklad řešení problému ohybu nosníku
V příkladu jsou vykresleny diagramy příčných sil a ohybových momentů, nalezen nebezpečný řez a vybrán I-nosník. V problému byla analyzována konstrukce diagramů pomocí diferenciálních závislostí, komparativní analýza různých průřezy trámy.

Příklad řešení problému kroucení hřídele
Úkolem je otestovat pevnost ocelového hřídele pro daný průměr, materiál a povolená napětí. Při řešení se sestavují diagramy momentů, smykových napětí a úhlů zkroucení. Vlastní hmotnost hřídele se nebere v úvahu

Příklad řešení problému tah-komprese tyče
Úkolem je otestovat pevnost ocelové tyče při daných dovolených napětích. Při řešení se sestavují grafy podélných sil, normálových napětí a posuvů. Vlastní hmotnost tyče se nebere v úvahu

Aplikace teorému zachování kinetické energie
Příklad řešení úlohy aplikace věty o zachování kinetické energie mechanické soustavy

Stanovení rychlosti a zrychlení bodu podle zadaných pohybových rovnic
Příklad řešení úlohy určení rychlosti a zrychlení bodu podle zadaných pohybových rovnic

Stanovení rychlostí a zrychlení bodů tuhého tělesa při planparalelním pohybu
Příklad řešení úlohy určování rychlostí a zrychlení bodů tuhého tělesa při planparalelním pohybu

Stanovení sil v rovinných příhradových prutech
Příklad řešení problému stanovení sil v prutech plochého vazníku Ritterovou metodou a metodou řezání uzlů.

státní autonomní instituce

Kaliningradská oblast

profesionální vzdělávací organizace

Vysoká škola služeb a cestovního ruchu

Průběh přednášek s ukázkami praktických úloh

"Základy teoretické mechaniky"

disciplínouTechnická mechanika

pro studenty3 kurs

speciality20.02.04 Požární bezpečnost

Kaliningrad

SCHVÁLIT

Zástupce ředitele pro SD GAU KO VEO KSTN.N. Myasnikov

SCHVÁLENÝ

Metodická rada GAU KO VET KST

POVAŽOVÁNO

Na schůzi PCC

Redakční tým:

Kolganova A.A., metodička

Falaleeva A.B., učitelka ruského jazyka a literatury

Cvetaeva L.V., předseda PCCobecné matematické a přírodovědné obory

Zkompilovaný:

Nezvanová I.V. Lektor GAU KO VET KST

Obsah

1. Teoretické informace

1. Teoretické informace

1. Příklady řešení praktických problémů

Dynamika: základní pojmy a axiomy

1. Teoretické informace

1. Příklady řešení praktických problémů

Bibliografie

Statika: základní pojmy a axiomy.

1. Teoretické informace

Statika - oddíl teoretické mechaniky, který se zabývá vlastnostmi sil působících na body tuhého tělesa a podmínkami jejich rovnováhy. Hlavní cíle:

1. Transformace soustav sil na ekvivalentní soustavy sil.

2. Stanovení podmínek pro rovnováhu soustav sil působících na tuhé těleso.

hmotný bod nazýván nejjednodušší model hmotného tělesa

jakýkoli tvar, jehož rozměry jsou dostatečně malé a který lze považovat za geometrický bod mající určitou hmotnost. Mechanický systém je jakýkoli soubor hmotných bodů. Absolutně tuhé těleso je mechanický systém, jehož vzdálenosti mezi body se při žádných interakcích nemění.

Síla je mírou mechanické interakce hmotných těles mezi sebou. Síla je vektorová veličina, protože je určena třemi prvky:

číselná hodnota;

směr;

aplikační bod (A).

Jednotkou síly je Newton (N).

Obrázek 1.1

Soustava sil je soubor sil působících na těleso.

Vyvážená (nulová) soustava sil je soustava, která při aplikaci na těleso nemění svůj stav.

Soustavu sil působících na těleso lze nahradit jednou výslednicí působící jako soustava sil.

Axiomy statiky.

Axiom 1: Pokud na těleso působí vyvážený systém sil, pak se pohybuje rovnoměrně a přímočarě nebo je v klidu (zákon setrvačnosti).

Axiom 2: Absolutně tuhé těleso je v rovnováze působením dvou sil právě tehdy, jsou-li tyto síly v absolutní hodnotě stejné, působí v jedné přímce a směřují v opačných směrech. Obrázek 1.2

Axiom 3: Mechanický stav tělesa se nenaruší, pokud se k soustavě sil, které na ně působí, přidá nebo odebere vyvážený systém sil.

Axiom 4: Výslednice dvou sil působících na těleso je rovna jejich geometrickému součtu, to znamená, že je vyjádřena v absolutní hodnotě a směru úhlopříčkou rovnoběžníku postaveného na těchto silách jako na stranách.

Obrázek 1.3.

Axiom 5: Síly, kterými na sebe dvě tělesa působí, jsou vždy stejné v absolutní hodnotě a směřují podél jedné přímky v opačných směrech.

Obrázek 1.4.

Typy vazeb a jejich reakce

spojení se nazývají jakákoli omezení, která brání pohybu těla v prostoru. Těleso, které se působením působících sil snaží pohnout, čemuž spojení brání, na něj bude působit určitou silou tzv. síla tlaku na spoj . Podle zákona o rovnosti akce a reakce bude spojení působit na těleso stejným modulem, ale opačně směrovanou silou.
Síla, kterou toto spojení působí na tělo a brání jednomu nebo druhému pohybu, se nazývá reakční síla (reakce) vazby .
Jedním ze základních principů mechaniky je osvobozenecký princip : jakékoli nesvobodné těleso lze považovat za volné, pokud vazby zahodíme a nahradíme jejich působení reakcemi vazeb.

Vazebná reakce je nasměrována opačným směrem, než kde vazba neumožňuje pohyb tělesa. Hlavní typy vazeb a jejich reakce jsou uvedeny v tabulce 1.1.

Tabulka 1.1

Typy vazeb a jejich reakce

Název komunikace

Symbol

1

Hladký povrch (podpora) - povrch (podpora), tření, o které lze dané těleso zanedbat.
S bezplatnou podporou, reakcesměřuje kolmo k tečně přes bodALE tělesný kontakt1 s opěrnou plochou2 .

2

Závit (pružný, neroztažitelný). Spojení, vytvořené ve formě neroztažitelného závitu, nedovolí, aby se tělo vzdalovalo od bodu zavěšení. Reakce závitu tedy směřuje podél závitu až do bodu jeho zavěšení.

3

beztížný prut – tyč, jejíž hmotnost lze ve srovnání s vnímanou zátěží zanedbat.
Reakce beztížné sklopné přímočaré tyče je směrována podél osy tyče.

4

Pohyblivý závěs, kloubová pohyblivá podpěra. Reakce je vedena podél normály k nosné ploše.

7

Pevné zavírání. V rovině tuhého uložení budou dvě složky reakce, a moment dvojice sil, která zabraňuje otáčení paprsku1 vzhledem k boduALE .
Pevné uchycení v prostoru odebere tělesu 1 všech šest stupňů volnosti - tři posunutí podél souřadnicových os a tři rotace kolem těchto os.
V prostorovém tuhém uložení budou tři komponenty, , a tři momenty párů sil.

Systém konvergujících sil

Systém konvergujících sil nazývá se soustava sil, jejichž akční linie se protínají v jednom bodě. Dvě síly sbíhající se v jednom bodě, podle třetího axiomu statiky, mohou být nahrazeny jednou silou -výsledný .
Hlavní vektor soustavy sil - hodnota rovna geometrickému součtu sil soustavy.

Výslednice rovinné soustavy sbíhajících se sil lze definovatgraficky a analyticky.

Sčítání soustavy sil . Sčítání ploché soustavy sbíhavých sil se provádí buď postupným sčítáním sil s konstrukcí mezilehlé výslednice (obr. 1.5), nebo konstrukcí silového mnohoúhelníku (obr. 1.6).

Obrázek 1.5Obrázek 1.6

Projekce síly na ose - algebraická veličina rovna součinu modulu síly a kosinu úhlu mezi silou a kladným směrem osy.
ProjekceFX(obr.1.7) síly na nápravu Xpozitivní, pokud je α akutní, negativní, pokud je α tupé. Pokud sílaje kolmá k ose, pak je její průmět na osu nulový.

Obrázek 1.7

Projekce síly na letadlo Oh- vektor , uzavřený mezi projekcemi začátku a konce sílydo této roviny. Tito. průmět síly do roviny je vektorová veličina charakterizovaná nejen číselnou hodnotou, ale i směrem v roviněOh (obr. 1.8).

Obrázek 1.8

Pak projekční modul do letadla Oh se bude rovnat:

Fxy = F cosα,

kde α je úhel mezi směrem síly a její projekce.
Analytický způsob zadávání sil . Pro analytickou metodu nastavení sílyje nutné zvolit systém souřadnicových osOhz, ve vztahu k němuž bude určen směr síly v prostoru.
Vektor znázorňující sílu, lze sestrojit, pokud jsou známy modul této síly a úhly α, β, γ, které síla svírá se souřadnicovými osami. TečkaALE použití síly nastavit samostatně svými souřadnicemiX, v, z. Sílu můžete nastavit jejími projekcemifx, fy, fzna souřadnicových osách. Modul síly je v tomto případě určen vzorcem:

a směrové kosiny:

, .

Analytická metoda sčítání sil : průmět součtového vektoru na nějakou osu je roven algebraickému součtu průmětů členů vektorů na stejnou osu, tj.

pak , , .
Vědět Rx, Ry, Rz, můžeme definovat modul

a směrové kosiny:

, , .

Obrázek 1.9

byl uzavřen (konec vektoru posledního členu

síla se musí shodovat se začátkem vektoru prvního členu síly). Potom bude hlavní vektor soustavy sil roven nule ()
2) Podmínky analytické rovnováhy . Modul hlavního vektoru soustavy sil je určen vzorcem. =0. Protože , pak se kořenový výraz může rovnat nule pouze tehdy, když každý člen současně zmizí, tzn.

Rx= 0, Ry= 0, R z = 0.

Pro rovnováhu prostorového systému sbíhajících se sil je tedy nutné a postačující, aby součty průmětů těchto sil na každou ze tří souřadnic os byly rovny nule:

Pro rovnováhu ploché soustavy konvergujících sil je nutné a postačující, aby součet průmětů sil na každou ze dvou souřadnicových os byl roven nule:

Sčítání dvou rovnoběžných sil ve stejném směru.

Obrázek 1.9

B A C

R=F 1 +F 2

Přidání dvou nestejných rovnoběžných sil nasměrovaných v opačných směrech.

Dvě nestejné antiparalelní síly jsou redukovány na jednu výslednou sílu rovnoběžnou s nimi a směřující k větší síle. Velikost výslednice je rovna rozdílu mezi velikostmi těchto sil a bod jejího působení, C, rozděluje vzdálenost mezi přímkami působení sil vně na části nepřímo úměrné velikostem těchto sil, že je

Dvojice sil a moment síly o bodu.

Moment síly vzhledem k bodu O se nazývá, bráno s příslušným znaménkem, součin velikosti síly se vzdáleností h od bodu O k přímce působení síly. . Tento produkt se bere se znaménkem plus, pokud je síla má tendenci otáčet tělo proti směru hodinových ručiček a se znaménkem -, pokud je síla má tendenci otáčet tělo ve směru hodinových ručiček, tzn . Délka kolmice h se nazývárameno síly bod O. Účinek působení síly tzn. úhlové zrychlení tělesa je tím větší, čím větší je velikost momentu síly.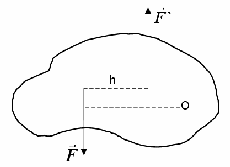

Obrázek 1.11

Zapisuje se takto: m(F, F")= ± F × h, kde součin je brán se znaménkem plus, pokud dvojice sil má tendenci otáčet těleso proti směru hodinových ručiček, a se znaménkem mínus, pokud dvojice sil má tendenci. pro otáčení těla ve směru hodinových ručiček.

Věta o součtu momentů sil dvojice.

Součet momentů sil dvojice (F,F“) vzhledem k libovolnému bodu 0 uvažovanému v rovině působení dvojice nezávisí na volbě tohoto bodu a je roven momentu dvojice.

Věta o ekvivalentních dvojicích. Důsledky.

Teorém. Dvě dvojice, jejichž momenty jsou si navzájem rovné, jsou ekvivalentní, tzn. (F, F") ~ (P, P")

Důsledek 1 . Dvojici sil lze přenášet do libovolného místa v rovině jejího působení, stejně jako ji natáčet do libovolného úhlu a měnit rameno a velikost sil dvojice při zachování momentu dvojice.

Důsledek 2. Dvojice sil nemá výslednici a nemůže být vyvážena jednou silou ležící v rovině dvojice.

Obrázek 1.12

Podmínka sčítání a rovnováhy pro soustavu dvojic v rovině.

1. Věta o sčítání dvojic ležících ve stejné rovině. Systém dvojic, libovolně umístěných ve stejné rovině, lze nahradit jednou dvojicí, jejíž moment je roven součtu momentů těchto dvojic.

2. Věta o rovnováze soustavy dvojic v rovině.

Aby absolutně tuhé těleso bylo v klidu působením soustavy dvojic, libovolně umístěných ve stejné rovině, je nutné a postačující, aby součet momentů všech dvojic byl roven nule, tzn.

Centrum gravitace

Gravitace - výslednice přitažlivých sil k Zemi, rozložená po celém objemu tělesa.

Těžiště těla - jedná se o takový bod, vždy spojený s tímto tělesem, kterým prochází přímka působení gravitační síly daného tělesa v libovolné poloze tělesa v prostoru.

Metody hledání těžiště

1. Metoda symetrie:

1.1. Pokud má homogenní těleso rovinu symetrie, pak těžiště leží v této rovině

1.2. Pokud má homogenní těleso osu symetrie, pak těžiště leží na této ose. Těžiště homogenního rotačního tělesa leží na ose rotace.

1.3 Pokud má homogenní těleso dvě osy souměrnosti, pak je těžiště v bodě jejich průsečíku.

2. Způsob dělení: Těleso se rozdělí na nejmenší počet dílů, jejichž gravitační síly a poloha těžišť jsou známy.

3. Metoda záporných hmotností: Při určování těžiště tělesa s volnými dutinami by měla být použita metoda rozdělování, ale hmotnost volných dutin by měla být považována za zápornou.

Souřadnice těžiště plochá postava:

Polohy těžišť jednoduchých geometrických obrazců lze vypočítat pomocí známých vzorců. (Obrázek 1.13)

Poznámka: Těžiště symetrie postavy je na ose souměrnosti.

Těžiště tyče je uprostřed výšky.

1.2. Příklady řešení praktických problémů

Příklad 1: Závaží je zavěšeno na tyči a je v rovnováze. Určete síly v tyči. (Obrázek 1.2.1)

Řešení:

Síly, které vznikají v upevňovacích tyčích, jsou co do velikosti stejné jako síly, kterými tyče nesou zatížení. (5. axiom)

Určíme možné směry reakcí vazeb "tuhé tyče".

Úsilí směřuje podél tyčí.

Obrázek 1.2.1.

Začněme konstrukci se známou silou nakreslením vektoruFv nějakém měřítku.

Od konce vektoruFnakreslete čáry rovnoběžné s reakcemiR 1 aR 2 .

Obrázek 1.2.2

Pro přesnější výpočty můžete použít geometrické vztahy, zejména sinusovou větu: poměr strany trojúhelníku k sinu opačného úhlu je konstantní hodnota

Pro tento případ:

Obrázek 1.2.3

Komentář: Pokud se směr vektoru (vazbová reakce) na daném schématu a v trojúhelníku sil neshodoval, pak by reakce na schématu měla směřovat opačným směrem.

Příklad 2: Analyticky určete velikost a směr výsledné ploché soustavy konvergujících sil.

Řešení:

Obrázek 1.2.4

Algebraickým sečtením průmětů získáme průmět výslednice na osu Ox.

Znaménko znamená, že výslednice je směrována doleva.

2. Určíme průměty všech sil na osu Oy:

Algebraickým sečtením průmětů dostaneme průmět výslednice na osu Oy.

Znaménko znamená, že výslednice směřuje dolů.

3. Určete modul výslednice pomocí velikostí průmětů:

4. Určete hodnotu úhlu výslednice s osou Ox:

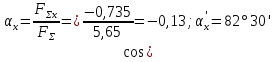
a hodnota úhlu s osou y:

Příklad 3: Vypočítejte součet momentů sil vzhledem k bodu O (obrázek 1.2.6).

OA= AB= VD=DE=CB=2m

Obrázek 1.2.6

Řešení:

1. Moment síly vzhledem k bodu je číselně roven součinu modulu a ramene síly.

2. Moment síly je roven nule, pokud čára působení síly prochází bodem.

Příklad 4: Určete polohu těžiště obrázku znázorněného na obrázku 1.2.7

Řešení:

Obrázek rozdělíme na tři:

1-obdélník

ALE 1 = 10 x 20 = 200 cm 2

2-trojúhelník

ALE 2 = 1/2 x 10 x 15 = 75 cm 2

3-kol

ALE 3 =3,14*3 2 = 28,3 cm 2

Obrázek 1 CG: x 1 = 10 cm, y 1 = 5 cm

Obrázek 2 CG: x 2 =20+1/3*15=25 cm, u 2 = 1/3 x 10 = 3,3 cm

Obrázek 3 CG: x 3 = 10 cm, y 3 = 5 cm

Je definován podobně pro S = 4,5 cm

Kinematika: základní pojmy.

Základní kinematické parametry

Trajektorie - čára, kterou hmotný bod ohraničuje při pohybu v prostoru. Trajektorie může být přímka a křivka, rovná a prostorová čára.

Rovnice trajektorie pro pohyb v rovině: y =F ( X)

Ujetá vzdálenost. Dráha se měří podél cesty ve směru jízdy. Označení -S, měrné jednotky - metry.

Rovnice pohybu bodu je rovnice, která určuje polohu pohybujícího se bodu jako funkci času.

Obrázek 2.1

Obrázek 2.2

V případě prostorového pohybu se přidává i třetí souřadnicez= F 3 ( t)

Tento druh pohybu se nazývákoordinovat .

Cestovní rychlost je vektorová veličina charakterizující v tento moment rychlost a směr pohybu po trajektorii.

Rychlost je vektor nasměrovaný v každém okamžiku tečně k trajektorii ve směru pohybu (obrázek 2.3).

Obrázek 2.3

Průměrná rychlost na cestě ΔSdefinovaný:

kde∆S- vzdálenost ujetá za čas Δt; Δ t- časový interval.

Pokud se bod pohybuje po nestejných drahách ve stejných časových intervalech, nazývá se pohybnerovný . V tomto případě je rychlost proměnná a závisí na časeproti= F( t)

Aktuální rychlost je definována jako

bodové zrychlení - vektorová veličina charakterizující rychlost změny rychlosti ve velikosti a směru.

Rychlost bodu při pohybu z bodu M1 do bodu Mg se mění ve velikosti a směru. Průměrná hodnota zrychlení za toto časové období

Aktuální zrychlení:

Obvykle se pro usnadnění uvažují dvě vzájemně kolmé složky zrychlení: normální a tangenciální (obrázek 2.4).

Normální zrychlení a n , charakterizuje změnu rychlosti tím

směr a je definován jako

Normální zrychlení je vždy směrováno kolmo na rychlost směrem ke středu oblouku.

Obrázek 2.4

Hodnota plného zrychlení je definována jako:

Analýza typů a kinematických parametrů pohybů

Jednotný pohyb - Jedná se o pohyb konstantní rychlostí:

Pro přímočarý rovnoměrný pohyb:

Pro křivočarý rovnoměrný pohyb:

Zákon rovnoměrného pohybu :

Rovnoměrně proměnný pohyb – je pohyb s konstantním tečným zrychlením:

Pro přímočarý rovnoměrný pohyb

Pro křivočarý rovnoměrný pohyb:

Zákon rovnoměrného pohybu:

Kinematické grafy

Kinematické grafy - jedná se o grafy změn dráhy, rychlosti a zrychlení v závislosti na čase.

Rovnoměrný pohyb (obrázek 2.5)

Obrázek 2.5

Rovnoměrně variabilní pohyb (obrázek 2.6)

Obrázek 2.6

Nejjednodušší pohyby tuhého tělesa

Pohyb vpřed nazývaný pohyb tuhého tělesa, při kterém jakákoli přímka na tělese během pohybu zůstává rovnoběžná s jeho výchozí polohou (obrázek 2.7)

Obrázek 2.7

Při translačním pohybu se všechny body těla pohybují stejným způsobem: rychlosti a zrychlení jsou v každém okamžiku stejné.

Vrotační pohyb všechny body těla popisují kružnice kolem společné pevné osy.

Pevná osa, kolem které se otáčejí všechny body tělesa, se nazýváosa otáčení.

Pouze pro popis rotačního pohybu tělesa kolem pevné osyrohové možnosti. (Obrázek 2.8)

φ je úhel natočení těla;

ω – úhlová rychlost, určuje změnu úhlu natočení za jednotku času;

Změna úhlové rychlosti s časem je určena úhlovým zrychlením:

2.2. Příklady řešení praktických problémů

Příklad 1: Je dána pohybová rovnice bodu. Určete rychlost bodu na konci třetí sekundy pohybu a průměrnou rychlost za první tři sekundy.

Řešení:

1. Rovnice rychlosti

2. Rychlost na konci třetí sekundy (t=3 C)

3. Průměrná rychlost

Příklad 2: Podle daného pohybového zákona určete druh pohybu, počáteční rychlost a tečné zrychlení bodu, čas do zastavení.

Řešení:

1. Typ pohybu: stejně variabilní ()
2. Při porovnávání rovnic je zřejmé, že

- počáteční dráha ujetá před začátkem odpočítávání 10m;

- počáteční rychlost 20m/s

- konstantní tečné zrychlení

- zrychlení je záporné, pohyb je tedy pomalý, zrychlení směřuje opačným směrem, než je rychlost pohybu.

3. Můžete určit čas, ve kterém bude rychlost bodu rovna nule.

3. Dynamika: základní pojmy a axiomy

Dynamika - úsek teoretické mechaniky, ve kterém se vytváří souvislost mezi pohybem těles a silami, které na ně působí.

V dynamice se řeší dva typy problémů:

určit parametry pohybu podle daných sil;

určit síly působící na těleso, podle daných kinematických parametrů pohybu.

Podhmotný bod implikují určité těleso, které má určitou hmotnost (tj. obsahuje určité množství hmoty), ale nemá lineární rozměry (nekonečně malý objem prostoru).
izolovaný uvažuje se hmotný bod, který není ovlivněn jinými hmotnými body. V reálném světě izolované hmotné body, stejně jako izolovaná těla, neexistují, tento koncept je podmíněný.

Při translačním pohybu se všechny body tělesa pohybují stejným způsobem, takže těleso lze brát jako hmotný bod.

Pokud jsou rozměry tělesa oproti dráze malé, lze jej považovat i za hmotný bod, přičemž bod splývá s těžištěm tělesa.

Při rotačním pohybu tělesa se body nemusí pohybovat stejným způsobem, v tomto případě lze některá ustanovení dynamiky aplikovat pouze na jednotlivé body a hmotný objekt lze považovat za soubor hmotných bodů.

Proto se dynamika dělí na dynamiku bodu a dynamiku hmotného systému.

Axiomy dynamiky

První axiom ( princip setrvačnosti): v každý izolovaný hmotný bod je ve stavu klidu nebo rovnoměrného a přímočarého pohybu, dokud ho aplikované síly z tohoto stavu nevyvedou.

Tento stav se nazývá státsetrvačnost. Odstraňte bod z tohoto stavu, tzn. dej tomu nějaké zrychlení, možná vnější sílu.

Každé tělo (bod) másetrvačnost. Mírou setrvačnosti je hmotnost tělesa.

Hmotnost volalamnožství hmoty v těle v klasické mechanice je považována za konstantní hodnotu. Jednotkou hmotnosti je kilogram (kg).

Druhý axiom (Druhý Newtonův zákon je základním zákonem dynamiky)

F=ma

kdet - hmotnost bodu, kg;A - bodové zrychlení, m/s 2 .

Zrychlení udělované hmotnému bodu silou je úměrné velikosti síly a shoduje se se směrem síly.

Gravitace působí na všechna tělesa na Zemi, uděluje tělu zrychlení volného pádu, směřujícího do středu Země:

G = mg

kdeG- 9,81 m/s², zrychlení volného pádu.

Třetí axiom (třetí Newtonův zákon): sSíly vzájemného působení dvou těles jsou stejné velikosti a směřují podél stejné přímky v různých směrech.

Při interakci jsou zrychlení nepřímo úměrné hmotnosti.

Čtvrtý axiom (zákon nezávislosti působení sil): doKaždá síla soustavy sil působí tak, jak by působila samostatně.

Zrychlení udělované bodu soustavou sil se rovná geometrickému součtu zrychlení udělovaných bodu každou silou zvlášť (obrázek 3.1):

Obrázek 3.1

Pojem tření. Druhy tření.

Tření- odpor vznikající při pohybu jednoho hrubého tělesa na povrchu druhého. Kluzné tření má za následek kluzné tření a valivé tření má za následek tření kývavé.

Kluzné tření

Obrázek 3.2.